Question

Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that $\Delta ABC \sim \Delta PQR$.

Answer 1

Hint: In $\Delta ABC$, extend AD to E and join thus getting a parallelogram ABEC. Similarly, extend PM to N and get parallelogram PQNR. Thus, prove that $\Delta ABE \sim \Delta PQN$, $\Delta ACE \sim \Delta PRN$. Hence by SAS similarity, $\Delta ABC \sim \Delta PQR$.

Complete step-by-step answer:
We have been given two triangles ABC and PQR. Now from the triangle, we can say that AD and PM are their medians. Now we have been told that 2 sides and median AD triangle ABC is proportional to 2 sides and median PM of triangle PQR.
Let us consider that AB and PQ are proportional and AC and PR are proportional from $\Delta ABC,\Delta PQR$. Then,
$\dfrac{{AB}}{{PQ}} = \dfrac{{AC}}{{PR}} = \dfrac{{AD}}{{PM}}$............…. (1)
Now let us produce AD to E, such that \[AD = DE\]. Similarly, produce PM to N such that $PM = MN$.
Now join BE, CE, QN, RN as shown in the figure.

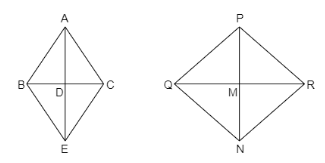
Thus, we get a quadrilateral ABEC and PQNR. They are parallelogram because their diagonals bisect each other at point D and M.
Now consider parallelogram ABEC and PQNR BE = AC and QN = PR, opposite sides of the parallelogram are equal. Hence, we can write it as,
$ \Rightarrow \dfrac{{BE}}{{AC}} = 1,\dfrac{{QN}}{{PR}} = 1$
Now from the above, we can say that,
$ \Rightarrow \dfrac{{BE}}{{AC}} = \dfrac{{QN}}{{PR}}$
Cross-multiply them,
$ \Rightarrow \dfrac{{AC}}{{PR}} = \dfrac{{BE}}{{QN}}$
Compare with equation (1),
$\therefore \dfrac{{AB}}{{PR}} = \dfrac{{BE}}{{QN}}$....................... (2)
From equation (1), $\dfrac{{AB}}{{PQ}} = \dfrac{{AD}}{{PM}}$
Multiply $\dfrac{{AD}}{{PM}}$ by 2,
$ \Rightarrow \dfrac{{AB}}{{PQ}} = \dfrac{{2AD}}{{2PM}}$
Substitute the values,
$ \Rightarrow \dfrac{{AB}}{{PQ}} = \dfrac{{AE}}{{PN}}$..................….. (3)
From equation (2) and (3),
$\therefore \dfrac{{BE}}{{QN}} = \dfrac{{AE}}{{PN}}$
By SSS similarity,
$\Delta ABE \sim \Delta PQN$
So, the corresponding angles of 2 triangles are equal.
$ \Rightarrow \angle BAE = \angle QPN$............….. (4)
Similarly, $\Delta ACE \sim \Delta PRN$.
So, the corresponding angles of 2 triangles are equal.
$ \Rightarrow \angle CAE = \angle RPN$..........….. (5)
Add the equations (4) and (5),
$ \Rightarrow \angle BAE + \angle CAE = \angle QPN + \angle RPN$
From the figure,
$ \Rightarrow \angle BAC = \angle BAE + \angle CAE,\angle QPR = \angle QPN + \angle RPN$
Substitute the values,
$\therefore \angle BAC = \angle QPR$.............….. (6)
Now, in $\Delta ABC$ and $\Delta PQR$,
$ \Rightarrow \dfrac{{AB}}{{PQ}} = \dfrac{{AC}}{{PR}}$ (from (1))
$ \Rightarrow \angle BAC = \angle QPR$ (from (6))
By SAS similarity,
$\therefore \Delta ABC \sim \Delta PQR$
Hence, it is proved.

Note: You should know the basic properties of triangles and parallelograms to solve a particular question like this. The entire question is based on their property. It is given 3 sides are proportional, you make think of moving I using SSS criterion, but that won’t be correct. Use SAS criterion to solve this problem. In SSS we compare all the three sides of a triangle. SAS is used to compare 2 sides and 1 angle.