Question

Show that voltage leads current by \[\dfrac{\pi }{2}\]​, when A.C. voltage applied to pure inductance.

Answer 1

Hint: First, find the instantaneous voltage in the coil with respect to time and angular velocity. Then, find the emf induced in the coil due to the change in current with respect to inductance and the rate of change of inductance. Then, apply Kirchhoff’s law and integrate the equations which conclude the result that voltage leads current by \[\dfrac{\pi }{2}\]​, when A.C. voltage applied to pure inductance.

Complete step-by-step answer:
Instantaneous voltage )
Voltage,
\[V=2\pi \sin \omega t\]
Where, \[\omega \] is the angular velocity, \[t\] is the time.
\[e=L\dfrac{dI}{dt}\]
Where, L is the inductance.

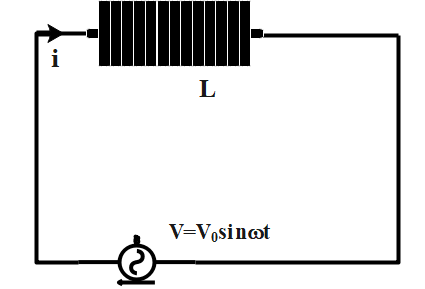
\[V\text{ }=\text{ }2\pi sin\omega t\]----- (1)
Let this be equation (1)
Where,
\[\omega \text{ }=\text{ }2\pi f\]
Voltage across the coil varies with time and the varying current induces an emf in the coil
From the Kirchhoff’s law, we can write
\[V\text{ }\text{ }e\text{ }=\text{ }0\]
Where, V is the voltage
e is the emf induced due to change in current
\[V\text{ }=\text{ }e\]----- (2)
Let this be equation (2)
Substitute the value of e as
\[e=L\dfrac{dI}{dt}\]in equation (2)
We get,
\[V=L\dfrac{dI}{dt}\]----- (3)
Let this be equation (3)
From the above equation, we obtain
\[dI=\text{ }V\dfrac{dt}{L}\]----- (4)
Let this be equation (4)
Substitute equation (1) in equation (4)
\[dI\text{ }=\text{ }\dfrac{{{V}_{0}}sin\omega tdt}{L}\]----- (5)
Let this be equation (5)
Integrating equation (5), we get
\[\int{dI=\dfrac{{{V}_{0}}}{L}}\int{\sin \omega tdt}\]----- (6)
Let it be equation (6)
Where, I is the current
We get,
\[I=\dfrac{{{V}_{o}}}{L}\dfrac{(-\cos \omega t)}{\omega }\] -----(7)
Let it be equation (7)
Then substitute,
\[-\cos \omega t=\sin (wt-\dfrac{\pi }{2})\] in equation (7)
Let \[\dfrac{{{V}_{o}}}{L\omega }={{I}_{0}}\] ----- (8)
Substitute equation (8) in equation (7)
We get,
\[I\text{ }={{I}_{o}}sin(\omega t-\dfrac{\pi }{2})\]----- (9)
Comparing equations (1) and (9),
We conclude that voltage leads current by \[\dfrac{\pi }{2}\]​, when A.C. voltage applied to pure inductance
Hence, proved.

Note: There is also a case where current leads voltage in phase by \[\dfrac{\pi }{2}\]. This happens in certain cases where an ideal capacitor is used in an A.C. circuit .Therefore, current leads voltage in phase by \[\dfrac{\pi }{2}\]​, in an A.C. circuit containing an ideal capacitor.