Question

Show that the function $f:R\to R:f(x)={{x}^{2}}$ is neither one-one nor onto.

Answer 1

Hint: To check whether the given function is one-one or not, assume two elements ${{x}_{1}}\text{ and }{{x}_{2}}$ in the set of the domain of the given function and substitute $f({{x}_{1}})=f({{x}_{2}})$. If ${{x}_{1}}={{x}_{2}}$, then $f(x)$ is one-one and if there is any more relation between ${{x}_{1}}\text{ and }{{x}_{2}}$ other than ${{x}_{1}}={{x}_{2}}$ then $f(x)$ is not one-one. To check whether the given function is onto or not, check that if the range of $f(x)$ is equal to co-domain or not. Here, co-domain is the set of all values of $f(x)$ in which the range of the function is constrained.

Complete step-by-step solution -
It is given that function is defined for all real numbers and overall real numbers. Therefore, both the domain and co-domain of the given function consist of the set of all real numbers.
First, let us show that the function is not one-one.
Assume two elements ${{x}_{1}}\text{ and }{{x}_{2}}$ in the set of the domain of the given function. Therefore,
\[f({{x}_{1}})=f({{x}_{2}})\]
Substituting, ${{x}_{1}}\text{ and }{{x}_{2}}$ in the function, we get,
\[\begin{align}
  & {{x}_{1}}^{2}={{x}_{2}}^{2} \\
 & \Rightarrow {{x}_{1}}^{2}-{{x}_{2}}^{2}=0 \\
 & \Rightarrow ({{x}_{1}}-{{x}_{2}})({{x}_{1}}+{{x}_{2}})=0 \\
 & \Rightarrow {{x}_{1}}-{{x}_{2}}=0\text{ or }{{x}_{1}}+{{x}_{2}}=0 \\
 & \Rightarrow {{x}_{1}}={{x}_{2}}\text{ or }{{x}_{1}}=-{{x}_{2}} \\
\end{align}\]
Clearly, we can see that, when \[f({{x}_{1}})=f({{x}_{2}})\] then, there is more than one relation between ${{x}_{1}}\text{ and }{{x}_{2}}$. Therefore, $f(x)$ is not one-one.
Now, let us show that the given function is not onto.
Clearly, we can see that the co-domain of the function contains the set of real numbers. Since$f(x)={{x}^{2}}$, therefore, the range of $f(x)$ will be only positive real numbers because the square of any real number will always be positive. So, here range and co-domain are not equal.
Therefore, it is proved that $f(x)$ is not onto.

Note: One may note that we do not have to cancel the common terms while checking whether the function is one-one. Consider all the possible relations between ${{x}_{1}}\text{ and }{{x}_{2}}$ and then only come to the conclusion just as we did in the above solution. Also, there is another method to check whether the given function is onto or not. We have to draw the graph of $f(x)={{x}^{2}}$ for all real values of ‘x’. If the graph of $f(x)={{x}^{2}}$ extends from $-\infty \text{ to }\infty $, that is it extends over all real numbers, then the function is onto otherwise not. Therefore, the graph of $f(x)={{x}^{2}}$ can be plotted as:

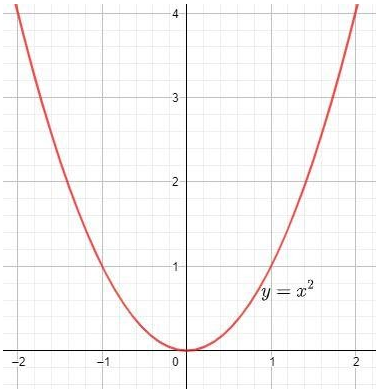
Clearly, we can see that the range of $f(x)={{x}^{2}}$ is from $\text{0 to }\infty $. Therefore, the given function is not onto.