Question

Show that the expression \[{{\tan }^{-1}}\dfrac{1}{2}+{{\tan }^{-1}}\dfrac{2}{11}={{\tan }^{-1}}\dfrac{3}{4}\] .

Answer 1

Hint: In the question, both LHS, as well as RHS, have the inverse of tan. First, we need to simplify it into simpler terms. Here, we consider \[A=\dfrac{1}{2}\] and \[B=\dfrac{2}{11}\]. For its simplification, we also know the formula \[{{\tan }^{-1}}A+{{\tan }^{-1}}B={{\tan }^{-1}}\left( \dfrac{A+B}{1-AB} \right)\] . Using this formula, we can transform these two inverse tan functions into a single tan inverse function as shown in RHS of the formula.

Complete step-by-step answer:
Now, according to the question, we have \[{{\tan }^{-1}}\dfrac{1}{2}+{{\tan }^{-1}}\dfrac{2}{11}\] in LHS.
Both terms in LHS have the inverse of tan.
Solving these two terms of inverse tan function by using the formula, we get
We know the formula, \[{{\tan }^{-1}}A+{{\tan }^{-1}}B={{\tan }^{-1}}\left( \dfrac{A+B}{1-AB} \right)\] .
In this formula, we have a single term in RHS. Also, according to the question, we have a single term in RHS. Here, this formula is best to be applied for simplification. So, this formula would be best here to get applied to obtain the required result.
Applying the above formula, we get
\[{{\tan }^{-1}}\dfrac{1}{2}+{{\tan }^{-1}}\dfrac{2}{11}\]
Now, transforming these two inverse tan functions into a single inverse tan function.
\[={{\tan }^{-1}}\left( \dfrac{\dfrac{1}{2}+\dfrac{2}{11}}{1-\dfrac{1}{2}.\dfrac{2}{11}} \right)\]
Taking 22 as LCM in numerator and denominator, we get
\[\begin{align}
  & {{\tan }^{-1}}\dfrac{1}{2}+{{\tan }^{-1}}\dfrac{2}{11} \\
 & ={{\tan }^{-1}}\left( \dfrac{\dfrac{1}{2}+\dfrac{2}{11}}{1-\dfrac{1}{2}.\dfrac{2}{11}} \right) \\
 & ={{\tan }^{-1}}\left( \dfrac{\dfrac{11+4}{22}}{\dfrac{22-2}{22}} \right) \\
 & ={{\tan }^{-1}}\left( \dfrac{15}{20} \right) \\
 & ={{\tan }^{-1}}\left( \dfrac{3}{4} \right). \\
\end{align}\]
Therefore, LHS=RHS.
So, \[{{\tan }^{-1}}\dfrac{1}{2}+{{\tan }^{-1}}\dfrac{2}{11}={{\tan }^{-1}}\dfrac{3}{4}\].
Hence, proved.

Note: In this question, one can think to find the principal values of the terms present in the LHS side. We don’t need to do that here. There is no need to find principal value. This question involves some calculations in the formula \[{{\tan }^{-1}}A+{{\tan }^{-1}}B={{\tan }^{-1}}\left( \dfrac{A+B}{1-AB} \right)\] , so we have to be attentive towards the calculation mistake.
We can also solve this question by converting the inverse of tan into the inverse of sine.
Assume,
\[{{\tan }^{-1}}\left( \dfrac{2}{11} \right)=y\] , \[{{\tan }^{-1}}\left( \dfrac{1}{2} \right)=x\] .
\[\begin{align}
  & {{\tan }^{-1}}\left( \dfrac{1}{2} \right)=x \\
 & \Rightarrow \tan x=\dfrac{1}{2} \\
\end{align}\]

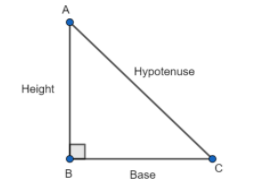
Using Pythagora's theorem, we can find the hypotenuse.
Hyptenuse = \[\sqrt{{{\left( Height \right)}^{2}}+{{\left( base \right)}^{2}}}\]
\[\begin{align}
  & =\sqrt{{{1}^{2}}+{{2}^{2}}} \\
 & =\sqrt{1+4} \\
 & =\sqrt{5} \\
\end{align}\]
\[\sin x=\dfrac{height}{hypotenuse}=\dfrac{1}{\sqrt{5}}\]
\[\cos x=\dfrac{base}{hypotenuse}=\dfrac{2}{\sqrt{5}}\]
Similarly,
 \[\begin{align}
  & {{\tan }^{-1}}\left( \dfrac{2}{11} \right)=y \\
 & \Rightarrow \dfrac{2}{11}=\tan y \\
\end{align}\]

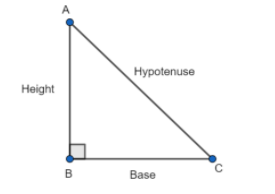
Using Pythagora's theorem, we can find the hypotenuse.
Hyptenuse = \[\sqrt{{{\left( Height \right)}^{2}}+{{\left( base \right)}^{2}}}\]
\[\begin{align}
  & =\sqrt{{{2}^{2}}+{{11}^{2}}} \\
 & =\sqrt{4+121} \\
 & =\sqrt{125} \\
\end{align}\]
\[\sin y=\dfrac{height}{hypotenuse}=\dfrac{2}{\sqrt{125}}\]
\[\cos y=\dfrac{base}{hypotenuse}=\dfrac{11}{\sqrt{125}}\]
We know the formula, \[\sin \left( x+y \right)=\sin x\cos y+\cos x\sin y\] .
Putting the value of \[\sin x\] , \[\cos x\] , \[\sin y\] , and \[\cos y\] in the above formula, we get
 \[\sin \left( x+y \right)=\sin x\cos y+\cos x\sin y\]
\[\begin{align}
  & \Rightarrow \sin \left( x+y \right)=\dfrac{1}{\sqrt{5}}.\dfrac{11}{\sqrt{125}}+\dfrac{2}{\sqrt{5}}.\dfrac{2}{\sqrt{125}} \\
 & \Rightarrow \sin \left( x+y \right)=\dfrac{11+4}{\sqrt{625}} \\
 & \Rightarrow \sin \left( x+y \right)=\dfrac{15}{25} \\
 & \Rightarrow \sin \left( x+y \right)=\dfrac{3}{5} \\
 & \Rightarrow \left( x+y \right)={{\sin }^{-}}\left( \dfrac{3}{5} \right) \\
\end{align}\]
Now, converting inverse of sine to inverse of tan.
Assume,
\[\begin{align}
  & z={{\sin }^{-1}}\left( \dfrac{3}{5} \right) \\
 & \Rightarrow \sin z=\dfrac{3}{5} \\
\end{align}\]

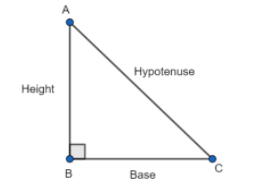
Using Pythagora's theorem, we can find the base.
Base = \[\sqrt{{{\left( hypotenuse \right)}^{2}}-{{\left( height \right)}^{2}}}\]
\[\begin{align}
  & =\sqrt{{{5}^{2}}-{{3}^{2}}} \\
 & =\sqrt{25-9} \\
 & =\sqrt{16} \\
 & =4 \\
\end{align}\]
\[\tan z=\dfrac{height}{base}=\dfrac{3}{4}\]
\[\begin{align}
  & \tan z=\dfrac{3}{4} \\
 & \Rightarrow z={{\tan }^{-1}}\left( \dfrac{3}{4} \right) \\
\end{align}\]
We have assumed, \[z={{\sin }^{-1}}\left( \dfrac{3}{5} \right)\] .
We can say that, \[z={{\sin }^{-1}}\left( \dfrac{3}{5} \right)={{\tan }^{-1}}\left( \dfrac{3}{4} \right)\] .
Also, we have, \[\left( x+y \right)={{\sin }^{-}}\left( \dfrac{3}{5} \right)\] .
So, \[\left( x+y \right)={{\tan }^{-1}}\left( \dfrac{3}{4} \right)\] .
Initially, we have assumed that \[{{\tan }^{-1}}\left( \dfrac{2}{11} \right)=y\] , \[{{\tan }^{-1}}\left( \dfrac{1}{2} \right)=x\] .
Therefore, \[{{\tan }^{-1}}\dfrac{1}{2}+{{\tan }^{-1}}\dfrac{2}{11}={{\tan }^{-1}}\dfrac{3}{4}\] .
Hence, proved.