Question

Show that the cone of the greatest volume which can be inscribed in a given sphere has an altitude equal to $\dfrac{2}{3}$ of the diameter of the sphere.

Answer 1

Hint: To solve this question, we have to remember the concept of maxima and minima of the application of derivatives. We will use the Pythagoras theorem according to the given situations.

Complete step-by-step solution:

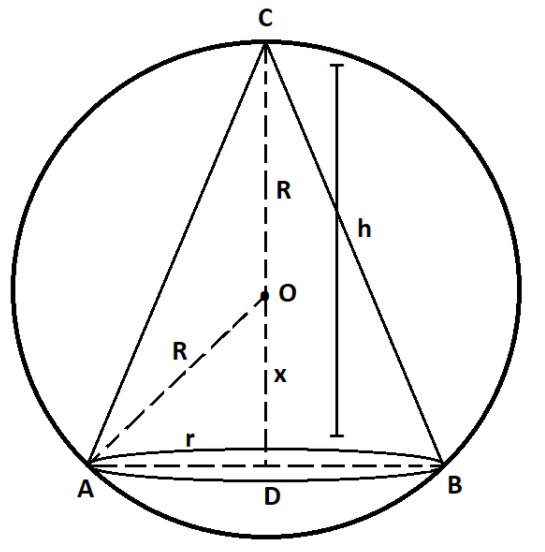
Let r be the radius and h be the height of the cone which is inscribed in a given sphere of radius R.
According to the question the sphere is given, i.e. R is constant.
Let OD = x.
Now, applying Pythagoras theorem in $\vartriangle OAD$,
We have,
$
   \Rightarrow {\left( {OA} \right)^2} = {\left( {OD} \right)^2} + {\left( {AD} \right)^2} \\
   \Rightarrow {R^2} = {x^2} + {r^2} \\
$
$ \Rightarrow {r^2} = {R^2} - {x^2}$..........................……… (i)
And from figure, we can see that
$h = R + x$.
We have to show that, the volume of the cone is greatest and altitude of cone is $\dfrac{2}{3}$ of diameter of sphere, i.e. h = $\dfrac{2}{3}\left( {2R} \right) = \dfrac{{4R}}{3}$.
We know that,
Volume of cone = $\dfrac{1}{3}\pi {r^2}h$
So,
$ \Rightarrow V = \dfrac{1}{3}\pi {r^2}h$
Putting the values of h and r, we will get
$ \Rightarrow V = \dfrac{1}{3}\pi \left( {{R^2} - {x^2}} \right)\left( {R + x} \right)$
Differentiating on both sides with respect to x, we will get
$
   \Rightarrow \dfrac{{dV}}{{dx}} = \dfrac{1}{3}\pi \left[ {\left( {{R^2} - {x^2}} \right) + \left( {R + x} \right)\left( { - 2x} \right)} \right] \\
   \Rightarrow \dfrac{{dV}}{{dx}} = \dfrac{1}{3}\pi \left( { - 3{x^2} - 2Rx + {R^2}} \right) \\
$
As we know that,
$\dfrac{{dV}}{{dx}} = 0$ [ for maxima and minima ].
Therefore,
$ \Rightarrow \dfrac{{dV}}{{dx}} = \dfrac{1}{3}\pi \left( { - 3{x^2} - 2Rx + {R^2}} \right) = 0$
We can solve this as:
$
   \Rightarrow 3{x^2} + 2Rx - {R^2} = 0 \\
   \Rightarrow 3{x^2} + 3Rx - Rx - {R^2} = 0 \\
   \Rightarrow 3x\left( {x + R} \right) - R\left( {x + R} \right) = 0 \\
   \Rightarrow \left( {3x - R} \right)\left( {x + R} \right) = 0 \\
$
Now, we can see that,
$\left( {x + R} \right) \ne 0$, thus $\left( {3x - R} \right) = 0$
$ \Rightarrow 3x = R$
$ \Rightarrow x = \dfrac{R}{3}$
From figure, we can see that
$ \Rightarrow h = x + R$
Putting value of x, we get
$ \Rightarrow h = \dfrac{R}{3} + R$
$ \Rightarrow h = \dfrac{{4R}}{3}$ [ proved ]
Now we have,
$ \Rightarrow \dfrac{{dV}}{{dx}} = \dfrac{1}{3}\pi \left( { - 3{x^2} - 2Rx + {R^2}} \right)$
Again differentiate both sides with respect to x, we will get
$ \Rightarrow \dfrac{{{d^2}V}}{{d{x^2}}} = \dfrac{1}{3}\pi \left( { - 6x - 2R} \right)$
Now,
$
   \Rightarrow {\left( {\dfrac{{{d^2}V}}{{d{x^2}}}} \right)_{x = \dfrac{R}{3}}} = \dfrac{1}{3}\pi \left( {\dfrac{{ - 6 \times R}}{3} - 2R} \right) \\
   \Rightarrow {\left( {\dfrac{{{d^2}V}}{{d{x^2}}}} \right)_{x = \dfrac{R}{3}}} = \dfrac{1}{3}\pi \left( { - 4R} \right) < 0 \\
$
We can clearly see that, $\dfrac{{{d^2}V}}{{d{x^2}}} < 0$.
Hence, we can say that the volume of the cone which is inscribed in a given sphere is greatest and the altitude of the cone is equal to $\dfrac{2}{3}$ of the diameter of the sphere.

Note: Whenever we ask this type of question, we have to remember the basic concepts of maxima and minima. First, we have to identify what we have given and what we have to assume. Then we will use the part which we have to prove and then by solving it with the help of a given part, we can easily prove the question. We have to remember that the critical values of V are given by $\dfrac{{dV}}{{dx}} = 0$. If n is even and ${f^n}\left( c \right) < 0$, then x = c is the point where $f\left( x \right)$ is maximum. And if n is even and ${f^n}\left( c \right) > 0$, then x = c is the point where $f\left( x \right)$ is minimum.