Question

Show that the altitude of the right circular cone of maximum volume that can be described in a sphere of radius r is $\dfrac{4r}{3}$. Also show that the maximum volume of the cone is $\dfrac{8}{27}$ of the volume of the sphere.

Answer 1

Hint: First, before proceeding for this, we must draw the sphere in which a cone is inscribed of maximum volume with radius R and height h of the cone. Then, by applying the Pythagoras theorem in triangle ABC, we get the relation between R, r and h. Then, calculate the maximum value of volume, we need to differentiate the above volume with respect to height as $\dfrac{dV}{dh}=0$which gives the value of h. Then, by using it, we get the relation between the volume of the sphere and cone.



Complete step-by-step answer:
In this question, we are supposed to show that the altitude of the right circular cone of maximum volume that can be described in a sphere of radius r is $\dfrac{4r}{3}$and also show that the maximum volume of the cone is $\dfrac{8}{27}$ of the volume of the sphere.
So, before proceeding for this, we must draw the sphere in which a cone is inscribed of maximum volume with radius R and height h of the cone and then proceed further as:

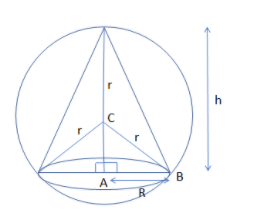
Now, from the figure, we can clearly see that value of AC as:
AC=h-r
So, by applying the Pythagoras theorem in triangle ABC, we get:
${{\left( h-r \right)}^{2}}+{{R}^{2}}={{r}^{2}}$
Now, we know the formula for the volume V of the cone is given by:
$V=\dfrac{1}{3}\pi {{R}^{2}}h$
Then, substituting the value of ${{R}^{2}}$as ${{r}^{2}}-{{\left( h-r \right)}^{2}}$ using Pythagoras relation in the above equation, we get:
$V=\dfrac{1}{3}\pi \left( {{r}^{2}}-{{\left( h-r \right)}^{2}} \right)h$
Then, by solving the above expression, we get:
$\begin{align}
  & V=\dfrac{1}{3}\pi \left( {{r}^{2}}-{{h}^{2}}-{{r}^{2}}+2hr \right)h \\
 & \Rightarrow V=\dfrac{1}{3}\pi \left( 2{{h}^{2}}r-{{h}^{3}} \right) \\
\end{align}$
Now, to calculate the maximum value of volume, we need to differentiate the above volume with respect to height as $\dfrac{dV}{dh}=0$.
So, by applying the above condition, we get:
$\dfrac{dV}{dh}=\dfrac{1}{3}\pi \left( 4hr-3{{h}^{2}} \right)$
Then, by equating it with zero, we get:
$\begin{align}
  & \dfrac{1}{3}\pi \left( 4hr-3{{h}^{2}} \right)=0 \\
 & \Rightarrow 4hr-3{{h}^{2}}=0 \\
 & \Rightarrow 4hr=3{{h}^{2}} \\
 & \Rightarrow 4r=3h \\
 & \Rightarrow h=\dfrac{4r}{3} \\
\end{align}$
So, we have proved that for the maximum volume of cones with height h inscribed in the sphere, we get the value of height as $\dfrac{4r}{3}$.
Then, by again differentiating the volume with respect to h, we get:
$\dfrac{{{d}^{2}}V}{d{{h}^{2}}}=\dfrac{1}{3}\pi \left( 4r-6h \right)$
Now, by substituting the value of h as $\dfrac{4r}{3}$ in above expression, we get:
$\begin{align}
  & \dfrac{{{d}^{2}}V}{d{{h}^{2}}}=\dfrac{1}{3}\pi \left( 4r-6\times \dfrac{4r}{3} \right) \\
 & \Rightarrow \dfrac{{{d}^{2}}V}{d{{h}^{2}}}=\dfrac{1}{3}\pi \left( 4r-8r \right) \\
 & \Rightarrow \dfrac{{{d}^{2}}V}{d{{h}^{2}}}=-\dfrac{1}{3}\pi 4r \\
\end{align}$
So, we get the negative result which shows that $h=\dfrac{4r}{3}$gives the maximum and the volume of the cone at $h=\dfrac{4r}{3}$will be maximum.
So, by substituting the value $h=\dfrac{4r}{3}$in the formula of the volume of the cone derived by applying pythagoras theorem as:
$V=\dfrac{1}{3}\pi \left( {{r}^{2}}-{{\left( \dfrac{4r}{3}-r \right)}^{2}} \right)\times \dfrac{4r}{3}$
Then, by solving the above equation, we get:
$\begin{align}
  & V=\dfrac{1}{3}\pi \left( {{r}^{2}}-\dfrac{16{{r}^{2}}}{9}-{{r}^{2}}+\dfrac{8{{r}^{2}}}{3} \right)\times \dfrac{4r}{3} \\
 & \Rightarrow V=\dfrac{1}{3}\pi \left( \dfrac{8{{r}^{2}}}{9} \right)\times \dfrac{4r}{3} \\
 & \Rightarrow V=\dfrac{8}{27}\left( \dfrac{4\pi {{r}^{3}}}{3} \right) \\
\end{align}$
Also, we know the formula for the volume of sphere is given by:
$\dfrac{4}{3}\pi {{r}^{3}}$
So, we get the relation that the volume of the cone is $\dfrac{8}{27}$times the volume of the sphere.

Note: To solve these types of questions we need to know some of the basic theorems as Pythagoras theorem beforehand to solve the question accurately. So, Pythagoras theorem says that in right angled triangle, the square of the hypotenuse h is equal to the sum of square of base b and height p of the triangle as:
${{h}^{2}}={{b}^{2}}+{{p}^{2}}$