Question

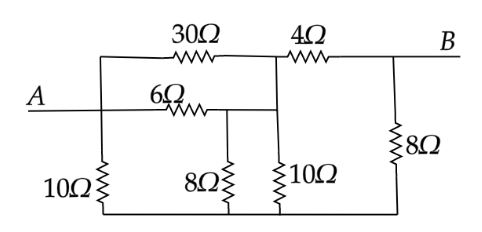
Seven resistors are connected as shown in the diagram: The equivalent resistance in ohms of this network between $A$ and $B$ is:

A. $6\Omega $
B. $8\Omega $
C. $12\Omega $
D. $20\Omega $

Answer 1

Hint: : Identify the parallel and series connection in the given circuit. First solve for the resistors in parallel connection, then the circuit will become a Wheatstone bridge. Check the condition for a balanced Wheatstone bridge.

Formula used:
Resistors connected in series, equivalence resistance ${R_{eq}} = {R_1} + {R_2} + {R_3} + ...$
Resistors connected in parallel, equivalence resistance $\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + ...$

Complete step by step answer:
First name the resistances and redraw the circuit diagram.

In the above circuit, we have to find the equivalent resistance between the terminal A and B.The resistors ${R_6}$ and ${R_7}$ are connected in parallel.Equivalence of ${R_6}$ and ${R_7}$ is given as
${R_{67}} = \dfrac{{{R_6} \cdot {R_7}}}{{{R_6} + {R_7}}}$
Substitute the values of ${R_6}$ and ${R_7}$ in the above formula.
$ \Rightarrow {R_{67}} = \dfrac{{8 \times 10}}{{8 + 10}}\Omega $
$ \Rightarrow {R_{67}} = \dfrac{{40}}{9}\Omega $
The resistors ${R_1}$ and ${R_5}$ are connected in parallel.
The equivalent resistor of ${R_1}$ and ${R_5}$ is given as
${R_{15}} = \dfrac{{{R_1} \cdot {R_5}}}{{{R_1} + {R_5}}}$
Substitute the values of ${R_1}$ and ${R_5}$ in the above formula.
$ \Rightarrow {R_{15}} = \dfrac{{30 \times 6}}{{30 + 6}}\Omega $
$\Rightarrow{R_{15}} = 5\Omega $

Now the equivalent circuit of above the circuit is as follows

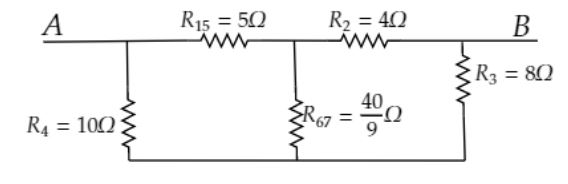
The equivalent circuit of the given circuit is a Wheatstone bridge circuit.
The Wheatstone bridge is balanced because it satisfies the condition $\dfrac{{{R_{15}}}}{{{R_4}}} = \dfrac{{{R_2}}}{{{R_3}}}$
Therefore, no current flows through the resistor ${R_{67}}$. Remove the ${R_{67}}$ from the Wheatstone bridge. The final circuit is as follows.

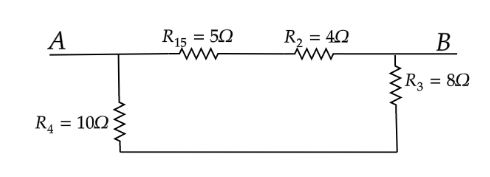
${R_{15}}$ and ${R_2}$ are in series.
The equivalent resistance of ${R_{15}}$ and ${R_2}$ is ${R_{152}} = {R_{15}} + {R_2}$
$ \Rightarrow {R_{152}} = 5\Omega + 4\Omega = 9\Omega $
${R_4}$ and ${R_3}$ are in series connection.
The equivalent resistance of ${R_4}$ and ${R_3}$ is ${R_{45}} = {R_4} + {R_5}$
$ \Rightarrow {R_{45}} = 10\Omega + 8\Omega = 18\Omega $
Now ${R_{152}}$ and ${R_{45}}$ are in parallel connection.
The equivalent resistance of ${R_{152}}$ and ${R_{45}}$ is \[{R_{eq}} = \dfrac{{{R_{152}} \cdot {R_{45}}}}{{{R_{152}} + {R_{45}}}}\].
Substitute the values of ${R_{152}}$ and ${R_{45}}$ in the above formula.
$ \Rightarrow {R_{eq}} = \dfrac{{9 \times 18}}{{9 + 18}}\Omega $
$\therefore {R_{eq}} = 6\Omega $
The equivalent resistance of the given circuit is $6\Omega $.

Hence the correct option is A.

Note: Alternative method:Alternatively, we can solve the circuit by drawing an equivalent circuit of the given circuit with some extra consideration as follows.

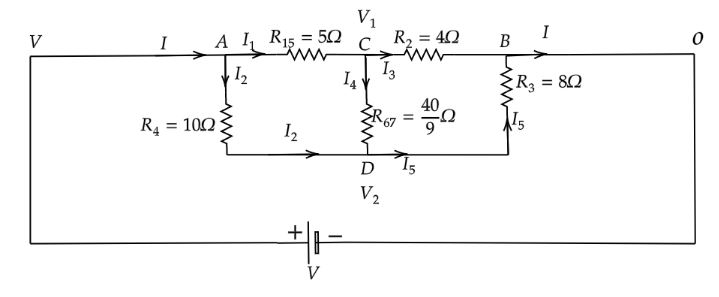
To solve the above equivalence circuit, Let the current $I$ enter junction A and leave junction B. A battery of $V$ voltage is connected across the terminals A and B. For simplification let terminal A is at $V$ voltage and terminal B is at $0$ voltage. Let the junctions C and D are at ${V_1}$ voltage and ${V_2}$ voltage respectively. Now apply Kirchhoff's current law at the junction A in the above equivalence circuit.
$I = {I_1} + {I_2}$

Apply Kirchhoff's current law at the junction C in the above equivalence circuit.
${I_1} = {I_3} + {I_4}$
From the above circuit diagram, ${I_1} = \dfrac{{V - {V_1}}}{5}$
${I_3} = \dfrac{{{V_1} - 0}}{4}$
$\Rightarrow {I_3} = \dfrac{{{V_1}}}{4}$
$\Rightarrow {I_4} = \dfrac{{{V_1} - {V_2}}}{{\dfrac{{40}}{9}}}$
$\Rightarrow {I_4} = \dfrac{9}{{40}}\left( {{V_1} - {V_2}} \right)$
Therefore,
\[\dfrac{{V - {V_1}}}{5} = \dfrac{{{V_1}}}{4} + \dfrac{9}{{40}}\left( {{V_1} - {V_2}} \right)\]
On simplification
$ \Rightarrow 27{V_1} - 9{V_2} = 8V$ …… (1)
Now apply Kirchhoff's current law at junction D in the above equivalence circuit.
${I_2} + {I_4} = {I_5}$

From the above circuit diagram, ${I_2} = \dfrac{{V - {V_2}}}{{10}}$
${I_5} = \dfrac{{{V_2} - 0}}{8}$
$\Rightarrow {I_5} = \dfrac{{{V_2}}}{8}$
Therefore,
\[\dfrac{{V - {V_2}}}{{10}} + \dfrac{9}{{40}}\left( {{V_1} - {V_2}} \right) = \dfrac{{{V_2}}}{8}\]
On simplification
$ \Rightarrow - 9{V_1} + 18{V_2} = 4V$ …… (2)
Now solve the two equations (1) and (2) and find the values of ${V_1}$ and ${V_2}$ in terms of $V$. We got,
${V_1} = \dfrac{{4V}}{9}$,
$\Rightarrow {V_2} = \dfrac{{4V}}{9}$

Now calculate the value of ${I_1} = \dfrac{{V - {V_1}}}{5}$
${I_1} = \dfrac{{V - \dfrac{{4V}}{9}}}{5}$
$\Rightarrow {I_1} = \dfrac{V}{9}$
And calculate the value of ${I_2} = \dfrac{{V - {V_2}}}{{10}}$
${I_2} = \dfrac{{V - \dfrac{{4V}}{9}}}{{10}}$
$\Rightarrow {I_2} = \dfrac{V}{{18}}$
Now we have $I = {I_1} + {I_2}$
Substitute the values of ${I_1}$ and ${I_2}$ in the above formula for $I$.
$I = \dfrac{V}{9} + \dfrac{V}{{18}}$

Further calculating
$ \Rightarrow I = \dfrac{V}{6}$
The equivalent resistance of the above equivalence circuit between the two terminals A and B is given by
${R_{eq}} = \dfrac{{{V_B} - {V_A}}}{I}$
Substitute all the required values in the above formula
${R_{eq}} = \dfrac{{V - 0}}{{\dfrac{V}{6}}}$
On further simplification
${R_{eq}} = 6\Omega $
Hence the correct option is (A).