Question

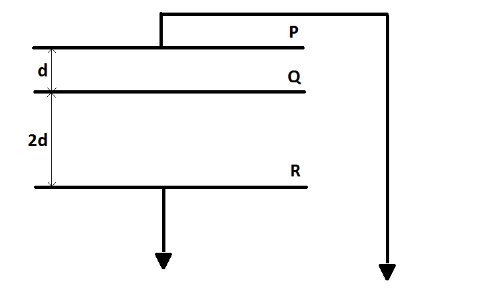
See the diagram. Area of each plate is $2.0{m^2}$and $d = 2 \times 10 \times {10^{ - 3}}m$. A charge of $8.85 \times {10^{ - 8}}C$ is given to Q. Then the potential difference of Q becomes

A. $13V$
B. $10V$
C. $66.7V$
D. $8.825V$

Answer 1

Hint:Here, we will consider the given circuit as two parallel capacitors. Therefore, we will first find out the net capacitance using the concept of parallel connection of capacitors. After that, by using the definition of capacitance, we will find the potential difference asked in the question.

Formulas used:
${C_{net}} = {C_1} + {C_2} = 100{\varepsilon _0} + 50{\varepsilon _0} = 150{\varepsilon _0}$$C = \dfrac{{{\varepsilon _0}A}}{d}$,
Where $C$ is the capacitance, ${\varepsilon _0}$ is the permittivity of free space, $A$ is area of plate and $d$ is the distance between two plates
${C_{net}} = {C_1} + {C_2}$,
Where ${C_{net}}$ is the net capacitance of two capacitors which are connected in parallel connection, ${C_1}$ is the capacitance of the first capacitor and ${C_2}$ is the capacitance of the second capacitor
\[C = \dfrac{Q}{V}\], where $C$is the capacitance, \[Q\] is the charge given and \[V\] is the potential difference

Complete step by step answer:
Considering the given circuit as the parallel connection of two capacitors, let the capacitance of both capacitors be ${C_1}$and ${C_2}$. Also, let ${Q_1}$and ${Q_2}$be the charge on these two capacitors.
For the first capacitor,
${C_1} = \dfrac{{{\varepsilon _0}A}}{d} \\
\Rightarrow{C_1}= \dfrac{{2{\varepsilon _0}}}{{20 \times {{10}^{ - 3}}}} \\
\Rightarrow{C_1}= 100{\varepsilon _0}\\$
And for the second capacitor,
${C_2} = \dfrac{{{\varepsilon _0}A}}{d} \\
\Rightarrow{C_2}= \dfrac{{2{\varepsilon _0}}}{{2 \times 20 \times {{10}^{ - 3}}}} \\
\Rightarrow{C_2}= 50{\varepsilon _0}\\$
Now, as ${C_1}$and ${C_2}$ are connected in parallel, the net capacitance is given by
${C_{net}} = {C_1} + {C_2} = 100{\varepsilon _0} + 50{\varepsilon _0} = 150{\varepsilon _0}$
It is given that total charge $Q = {Q_1} + {Q_2} = 8.85 \times {10^{ - 8}}C$
From the definition of capacitor, \[C = \dfrac{Q}{V}\]
Therefore, \[V = \dfrac{Q}{C}\]
We will take the net capacitance in this equation
$ V = \dfrac{Q}{{{C_{net}}}}\\
\Rightarrow V = \dfrac{{8.85 \times {{10}^{ - 8}}}}{{150{\varepsilon _0}}}\\$
We know that permittivity of free space ${\varepsilon _0} = 8.85 \times {10^{ - 12}}$
$ \Rightarrow V = \dfrac{{8.85 \times {{10}^{ - 8}}}}{{150 \times 8.85 \times {{10}^{ - 12}}}}\\
 \Rightarrow V = 0.006667 \times {10^4}\\
 \therefore V= 66.7V\\$
Thus, the potential difference of Q becomes $66.7V$

Hence, option C is the right answer.

Note:Most of the students gets confused in between the series and parallel combination of formula for capacitors so always remember that we have used the concept of parallel connection of capacitors in which the net capacitance is given as:
${C_{net}} = {C_1} + {C_2}$
Similarly, when the capacitors are connected in series, their net capacitance is given by:
$
\dfrac{1}{{{C_{net}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} = \dfrac{{{C_1} + {C_2}}}{{{C_1}{C_2}}} \\
\Rightarrow {C_{net}} = \dfrac{{{C_1}{C_2}}}{{{C_1} + {C_2}}} \\
$