Question

Same current ‘I’ is flowing in the three infinitely long wire along positive x, y and z directions. The magnetic field at a point (0, 0, -a) would be:
$\begin{align}
  & A.\text{ }\dfrac{{{\mu }_{0}}i}{2\pi a}\left( \widehat{j}-\widehat{i} \right) \\
 & B.\text{ }\dfrac{{{\mu }_{0}}i}{2\pi a}\left( \widehat{i}+\widehat{j} \right) \\
 & C.\text{ }\dfrac{{{\mu }_{0}}i}{2\pi a}\left( \widehat{i}-\widehat{j} \right) \\
 & D.\text{ }\dfrac{{{\mu }_{0}}i}{2\pi a}\left( \widehat{i}+\widehat{j}+\widehat{k} \right) \\
\end{align}$

Answer 1

Hint: First locate point (0, 0, -a) and then apply magnetic field formula along X, Y and Z axis. This will give us the solution for the three infinitely long wires along the 3 – axis given in the question.

Formula used:
$B=\dfrac{{{\mu }_{o}}I}{2\pi r}$

Complete step by step solution:
First let’s locate point A (0, 0, -a) on the axis as shown in the figure.

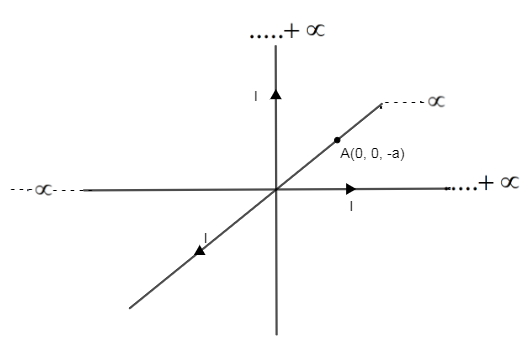
As we can say in the figure point A is located on the -Z- axis
Current directions are in +Z -axis as shown in the figure.

Now the magnitude field at point A is,
$\overrightarrow{{{B}_{A}}}=\overrightarrow{{{B}_{X}}}+\overrightarrow{{{B}_{Y}}}+\overrightarrow{{{B}_{Z}}}...\left( 1 \right)$
Where, $\overrightarrow{{{B}_{A}}}$ = magnetic field at point A.
$\overrightarrow{{{B}_{X}}}$= magnetic field due to X- axis
$\overrightarrow{{{B}_{Y}}}$= magnetic field due to Y-axis
$\overrightarrow{{{B}_{Z}}}$= magnetic field due to Z-axis
Now let’s find$\overrightarrow{{{B}_{X}}}$,

Formula for the magnetic field is,
$\Rightarrow B=\dfrac{{{\mu }_{o}}I}{2\pi r}$
Where, B = magnetic field
${{\mu }_{o}}=$ Permeability of the free space
r = distance from the wire to the point.
Here r will be taken as ‘a’ for $\overrightarrow{{{B}_{X}}}$
$\overrightarrow{{{B}_{X}}}=\left( \dfrac{{{\mu }_{o}}I}{2\pi a} \right)\widehat{j}$
Direction of $\overrightarrow{{{B}_{X}}}$is in $\widehat{j}$ direction.

Now similarly,
$\overrightarrow{{{B}_{Y}}}=\left( \dfrac{{{\mu }_{o}}I}{2\pi a} \right)\left( -\widehat{i} \right)$
Direction of $\overrightarrow{{{B}_{Y}}}$will be $\left( -\widehat{i} \right)$direction.

Now, $\overrightarrow{{{B}_{Z}}}$will be zero because the point A (0, 0, -a) lies on the Z-axis itself.
${{B}_{Z}}=O$

Now let’s put all the values in equation (1)
$\begin{align}
  & \Rightarrow \overrightarrow{{{B}_{A}}}=\left( \dfrac{{{\mu }_{o}}I}{2\pi a} \right)\widehat{j}+\left( \dfrac{{{\mu }_{o}}I}{2\pi a} \right)\widehat{i}+o \\
 & \therefore \overrightarrow{{{B}_{A}}}=\left( \dfrac{{{\mu }_{o}}I}{2\pi a} \right)\left( \widehat{j}-\widehat{i} \right) \\
\end{align}$

Hence the correct option is (A) $\left( \dfrac{{{\mu }_{o}}I}{2\pi a} \right)\left( \widehat{j}-\widehat{i} \right)$,

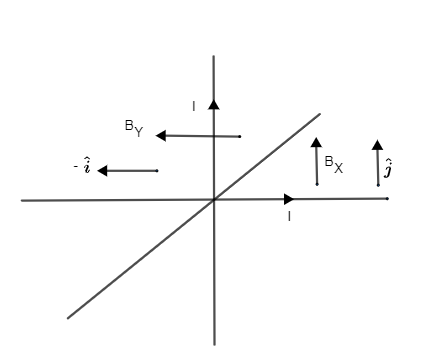
Note:
When we are giving direction for the magnitude fields don’t mistake directions given for $\widehat{i}$ as ${{B}_{X}}$ because it is in the X direction use the thumb rule for the direction of the magnetic field as shown in figure.