Question

Related to the numerical method, what is the formula by the trapezoidal rule?

Answer 1

Hint: For answering this we will understand how we integrate any function from the lower limit to the upper limit and how this integration can be calculated using the trapezoidal rule.

Complete step-by-step answer:
Given:
We have to give the formula of the definite integral of any function as per the trapezoidal rule.
Now, first, we will understand the geometrical meaning of $\int\limits_{x=a}^{x=b}{f\left( x \right)}dx$ . If there is any function $y=f\left( x \right)$ then, $\int\limits_{x=a}^{x=b}{f\left( x \right)}dx$ represents the algebraic sum of the area between $y=f\left( x \right)$ and $x-axis$ from $x=a$ to $x=b$ and the area above $x-axis$ will be treated as positive and area below $x-axis$ will be treated as negative. For more clarity look at the below figure:

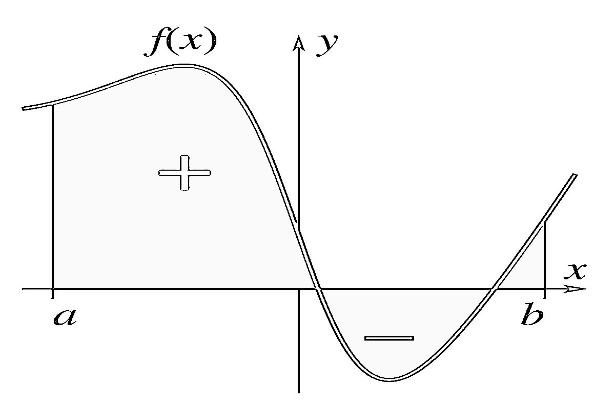
Now, for any function, there are many methods to find this area and out of them, an important integration rule is a “Trapezoidal Rule”, which is used for approximating the definite integrals by using the linear approximation of $y=f\left( x \right)$ . However, it gives the exact result in the case of linear functions.
Trapezoidal Rule:
Trapezoidal rule is a rule that evaluates the area under the curve by dividing the total area into smaller strips of trapezium shape. Then the area of each strip is found separately. Then the area under the curve and the $x-axis$ from $x=a$ to $x=b$ is approximately equal to the area of these trapeziums. For better understanding look at the picture given below:

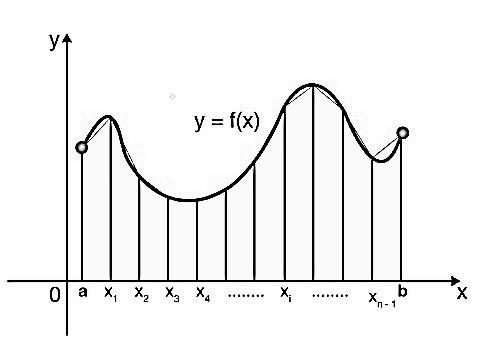
Trapezoidal Rule Formula:
Let, $y=f\left( x \right)$ be any function and $x={{x}_{0}}=a$ , $x={{x}_{n}}=b$ then, the area between the curve $y=f\left( x \right)$ and the $x-axis$ from $x=a$ to $x=b$ will be $\int\limits_{x=a}^{x=b}{f\left( x \right)}dx$ . According to Trapezoidal rule:
$\int\limits_{x=a}^{x=b}{f\left( x \right)}dx=\dfrac{h}{2}\left[ \left( f\left( {{x}_{0}} \right)+f\left( {{x}_{n}} \right) \right)+2\left( f\left( {{x}_{1}} \right)+f\left( {{x}_{2}} \right)+f\left( {{x}_{3}} \right)+................+f\left( {{x}_{n-1}} \right) \right) \right]$
Where, $h=\dfrac{{{x}_{n}}-{{x}_{0}}}{n}$ and $h$ is called as step-size and $n$ is the number of steps.

Note: Here, the geometrical meaning of $\int\limits_{x=a}^{x=b}{f\left( x \right)}dx$ should be clear to the student. And the concept which is involved in the derivation of the Trapezoidal rule formula should be used without any mistake and clarity to understand the result. Moreover, we should try to visualize the concepts of calculus and try to understand it with more clarity.