Question

Reflection of the point $\left( \alpha ,\beta ,\gamma \right)$ in the XY plane is:
a). $\left( -\alpha ,\beta ,\gamma \right)$
b). $\left( \alpha ,\beta ,0 \right)$
c). $\left( 0,0,\gamma \right)$
d). $\left( \alpha ,\beta ,-\gamma \right)$

Answer 1

Hint: We will use the concept of 3-D geometry to find the reflection of point $\left( \alpha ,\beta ,\gamma \right)$in the XY plane. We will use the concept that when we take the reflection of any point in the XY plane then the x and y coordinate of the point remains the same and z-coordinate changes only in sign but magnitude remains the same.

Complete step-by-step solution:
From the question we can see that $\left( \alpha ,\beta ,\gamma \right)$ is a point which lies in the 3-D plane. Since, we have to find the reflection of point $\left( \alpha ,\beta ,\gamma \right)$in the XY plane.
Let us assume that ADCB is an XY plane and point E $\left( \alpha,\beta,\gamma \right)$ be the point that lies above the plane XY.

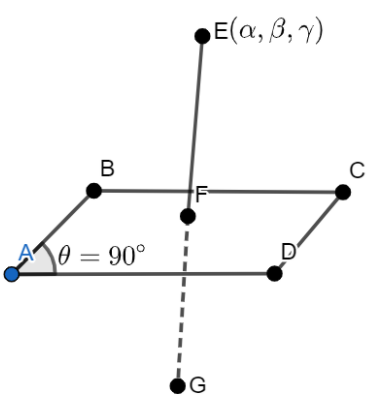
Let us say that AD is the x-axis and AB is the y-axis and AD is perpendicular to AB.
So, the distance of point E from the x-axis is $\alpha $, and the distance of point E from the y-axis is $\beta $ and that from the z-axis is $\gamma $.
Now, when we take the reflection of point E in the XY plane ADCB then we will get point G.
So, we can say that we have to move the same distance $\alpha $ on the x-axis(i.e. on line AD) and on the y-axis, we will also move the same $\beta $ distance but since G is opposite to E so we have to move in an opposite direction on the z-axis to reach point G but its magnitude is same as that of $\gamma $.
So, we can say that the point G is $\left( \alpha ,\beta ,-\gamma \right)$.
Hence, option(d) is the correct answer.

Note: Students are required to note that when we take the reflection of any point about XY then only the sign of z-coordinate changes and the rest of the coordinates remains the same. Similarly, when we take a reflection of point about YZ axis then the sign of only x-coordinate changes and the rest of things remains the same. Similarly, when we take a reflection of point about XZ axis then sign of y-coordinates changes only, and remaining coordinates remain the same as it is before.