Question

Rain water, which falls on a flat rectangular surface of length $ 6\;m $ and breadth $ 4\;m $ is transferred into a cylindrical vessel of internal radius $ 20\;cm. $ What will be the height of water in the cylindrical vessel if a rainfall of $ 1\;cm $ has fallen? $ \left( {Use\,\,\pi = \dfrac{{22}}{7}} \right) $

Answer 1

Hint: To find require height of cylindrical vessel we first find volume of water accumulate on rectangular roof and then equating this volume of water to volume of cylindrical vessel as all water which accumulate on roof transferred to cylindrical vessel and then substituting given values in formulas to find value of h or height of cylindrical vessel.
Formulas used: Volume of cuboid $ L \times B \times H $ , Volume of cylinder = $ \pi {r^2}h $

Complete step-by-step answer:
Given that
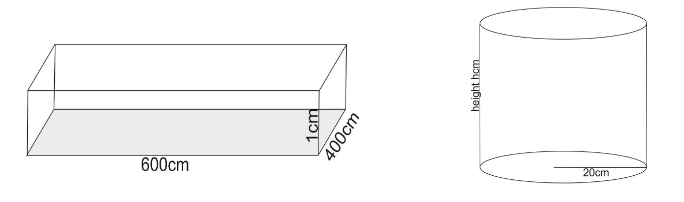
Length and breadth of a flat rectangular surface area $ 6\;m\,\,and\,\,4\;m $ respectively.
Or we have
Length = $ 600\;cm $
Breadth = $ 400\;cm $
Since, there has been a rainfall of $ 1\;cm $ .
Therefore, water accumulates on the roof in the shape of a cuboid of dimension $ 600\;cm,400\;cm\,by\,1\;cm $ .
Hence, quantity of water accumulate on rectangular roof is given as: $ L \times B \times H $
Substituting values in above we get volume of water on roof = $ 600 \times 400 \times 1 $
 $ \Rightarrow $ Volume of water on roof = $ 240000 $ $ c{m^3} $

Since, all this water accumulates on the roof is transferred to a cylindrical vessel.
Therefore, the volume of water accumulated on the roof will be equal to the volume of water going in the cylindrical vessel.
 $ \Rightarrow $ Volume of water accumulate on root = $ \pi {r^2}h $
Substituting values in above we have,
 $
  240000 = \dfrac{{22}}{7} \times {\left( {20} \right)^2} \times h \\
   \Rightarrow \dfrac{{2400000 \times 7}}{{22 \times 20 \times 20}} = h \\
   \Rightarrow h = 191 \;
  $
Therefore, from above we see that the height of water level in a cylindrical vessel is $ 191\;cm\,\,or\,\,1.91\;m $ .
So, the correct answer is “191 cm or 1.91 m”.

Note: In this type of problem in which quantity of liquid when transferred from one figure to other figure, then we can equate volume of two figures so used and then substituting given values and simplifying to get unknown or required value of given problem.