Question

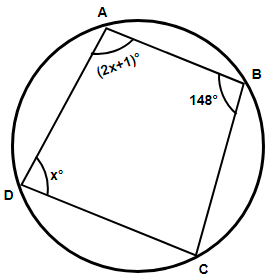
Quadrilateral ABCD is inscribed on the circle. What is the measure of angle A?

Answer 1

Hint: Use the property of a cyclic quadrilateral that ’the sum of opposite angles of cyclic quadrilateral measures 180 degrees’. Consider the angles B and D, take their sum and equate them with 180 degrees to calculate the value of x. Once the value of x is determined, substitute it in the given expression of angle A to get the answer.

Complete step by step solution:
Here we have been provided with a quadrilateral ABCD inscribed in a circle and we are asked to determine the measurement of angle A. Let us use the property of a cyclic quadrilateral.
Now, a quadrilateral is called a cyclic quadrilateral if all of its four vertices lie on the circumference of the circle. In the figure shown below we have all the four vertices A, B, C and D of the quadrilateral lying on the circumference of the circle, so we can say that ABCD is a cyclic quadrilateral.

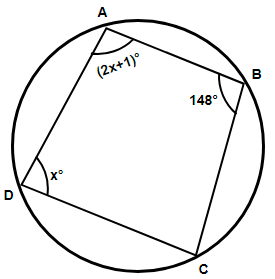
Now, we know that the sum of opposite angles of a cyclic quadrilateral is 180 degrees, so considering angles B and D we must have mathematically,
\[\Rightarrow \angle B+\angle D={{180}^{\circ }}\]
Substituting the known values from the figure we get,
\[\begin{align}
  & \Rightarrow {{148}^{\circ }}+x={{180}^{\circ }} \\
 & \Rightarrow x={{180}^{\circ }}-{{148}^{\circ }} \\
 & \Rightarrow x={{32}^{\circ }} \\
\end{align}\]
As we can see that we have been provided with the expression of angle A in terms of x as $\angle A=\left( 2x+1 \right)$, so substituting the value of x we get,
$\begin{align}
  & \Rightarrow \angle A=\left( 2\left( 32 \right)+1 \right) \\
 & \Rightarrow \angle A=\left( 64+1 \right) \\
 & \therefore \angle A={{65}^{\circ }} \\
\end{align}$
Hence, the measure of angle A is 65 degrees.

Note: Note that if you are asked to find the measure of angle C at the end then you have two ways to get the answer. First way is to consider angles A and C and use the same property of the cyclic quadrilateral that we have used in the above solution. In the second method you can use the property of a general quadrilateral that the sum of interior angles of a quadrilateral is 360 degrees. Remember that the property we have used to solve the question is proved using the other important property of a circle which states that ‘equal arcs subtend equal angles at the circumference of the circle’.