Question

P-V diagram of an ideal gas is given in the figure

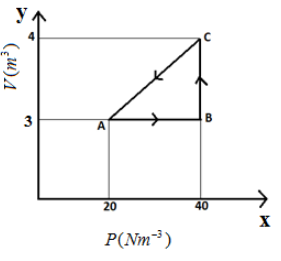
Work done on the gas in process CA is
A. $60J$
B. $70J$
C. $30J$
D. $20J$

Answer 1

Hint:In a cyclic process, the total work done is equal to the area enclosed by the graph. The work done will be positive if the cycle is going in clockwise direction and negative if the cycle is going in an anti-clockwise direction.

Formula used:
$W = \dfrac{{({P_f} + {P_i})}}{2}\Delta V$
Where $W$ is the total work done, ${P_i}$ is the initial pressure, ${P_f}$ is the final pressure and $\Delta V$ is the change in volume.

Complete step by step solution:
In the above cyclic process, while going from C to A, we can notice that it is a straight line that is both the volume and pressure are changing. We can obtain the total work done in this in a similar way we find the work done for an adiabatic process which is $P\Delta V$ where $P$ is the pressure and $\Delta V$ is the change in volume of the gas. But instead of constant pressure $P$, we consider the average pressure $\dfrac{{({P_f} + {P_i})}}{2}$ .
Thus we obtain the formula $W = \dfrac{{({P_f} + {P_i})}}{2}\Delta V$ .
It the above figure, it is given the value of initial pressure ${P_i}$ as $20N{m^{ - 3}}$ , final pressure ${P_f}$ as $40N{m^{ - 3}}$ and we can obtain the change in volume $\Delta V$ as $1{m^3}$ .
By substituting these values in the above formula, we get
$W = \left( {\dfrac{{20 + 40}}{2}} \right) \times 1 = 30J$

So,the correct option is C.

Note:For a cyclic process that is going in anti-clockwise direction, the total work is negative. The total work done can be found by summing up all the works done in A to B, B to C and C to A or by finding the area enclosed by the graph.