
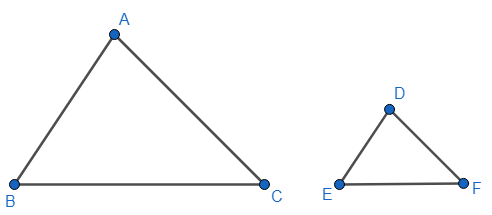
Puneet prepared two posters on ‘National Integration’ for decoration on Independence Day on triangular sheets (say ABC and DEF). The sides AB and AC and the perimeter ${{P}_{1}}$ of $\Delta ABC$ are respectively three times the corresponding sides DE and DF and the perimeter ${{P}_{2}}$ of $\Delta DEF$. Are the two triangular sheets similar? If yes, find $\dfrac{ar\left( \Delta ABC \right)}{ar\left( \Delta DEF \right)}$.
What values can be inculcated through celebration of national festivals?

Answer
521.7k+ views
Hint: We know that the perimeter of a triangle is the sum of all three sides of that triangle. Using this definition and the information given in the question, we must check whether the two triangles are similar or not. Also, we know that the ratio of areas of two similar triangles is the square of the ratio of corresponding sides.
Complete step-by-step solution:
We have the following two triangles, ABC and DEF.
It is also given to us that the line segments AB and AC are three times the corresponding sides DE and DF respectively.
We can write this mathematically as
$AB=3DE$
$AC=3DF$
We are also given that the perimeter of triangle ABC, ${{P}_{1}}$ is three times the perimeter of triangle DEF, ${{P}_{2}}$. Hence, we have
${{P}_{1}}=3{{P}_{2}}$
We know that the perimeter of a triangle is the sum of all 3 sides of a triangle.
Hence, we can write the above equation as
$\left( AB+AC+BC \right)=3\left( DE+DF+EF \right)$
Using the values of AB and AC, we can write
\[3DE+3DF+BC=3DE+3DF+3EF\]
On cancelling the terms, we get
$BC=3EF$
Now, in $\Delta ABC\text{ and }\Delta DEF$, we can very easily see that
$\dfrac{AB}{DE}=\dfrac{BC}{EF}=\dfrac{AC}{DF}=\dfrac{3}{1}$
Since the corresponding sides are in the same ratio, we can write that by SSS similarity, $\Delta ABC\text{ and }\Delta DEF$ are similar to each other.
We also know that the ratio of areas of two similar triangles is equal to the square of the ratio of corresponding sides.
Hence, we can write that
$\dfrac{ar\left( \Delta ABC \right)}{ar\left( \Delta DEF \right)}={{\left( \dfrac{AB}{DE} \right)}^{2}}$
Hence, we get
$\dfrac{ar\left( \Delta ABC \right)}{ar\left( \Delta DEF \right)}=9$
The values that can be inculcated through celebration of national festivals are unity of the nation, fraternity and patriotism.
Note: We must remember that we need to find the ratio $\dfrac{ar\left( \Delta ABC \right)}{ar\left( \Delta DEF \right)}$ and not $\dfrac{ar\left( \Delta DEF \right)}{ar\left( \Delta ABC \right)}$. Also, we must take utmost care while writing the corresponding sides, as it is very easy to mistake at this point. We can see that the last part of this question is a value-based question.
Complete step-by-step solution:
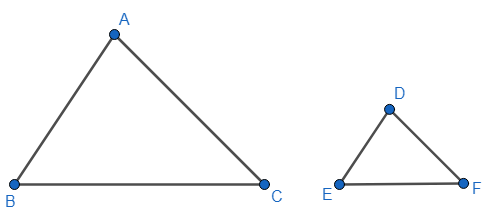
We have the following two triangles, ABC and DEF.

It is also given to us that the line segments AB and AC are three times the corresponding sides DE and DF respectively.
We can write this mathematically as
$AB=3DE$
$AC=3DF$
We are also given that the perimeter of triangle ABC, ${{P}_{1}}$ is three times the perimeter of triangle DEF, ${{P}_{2}}$. Hence, we have
${{P}_{1}}=3{{P}_{2}}$
We know that the perimeter of a triangle is the sum of all 3 sides of a triangle.
Hence, we can write the above equation as
$\left( AB+AC+BC \right)=3\left( DE+DF+EF \right)$
Using the values of AB and AC, we can write
\[3DE+3DF+BC=3DE+3DF+3EF\]
On cancelling the terms, we get
$BC=3EF$
Now, in $\Delta ABC\text{ and }\Delta DEF$, we can very easily see that
$\dfrac{AB}{DE}=\dfrac{BC}{EF}=\dfrac{AC}{DF}=\dfrac{3}{1}$
Since the corresponding sides are in the same ratio, we can write that by SSS similarity, $\Delta ABC\text{ and }\Delta DEF$ are similar to each other.
We also know that the ratio of areas of two similar triangles is equal to the square of the ratio of corresponding sides.
Hence, we can write that
$\dfrac{ar\left( \Delta ABC \right)}{ar\left( \Delta DEF \right)}={{\left( \dfrac{AB}{DE} \right)}^{2}}$
Hence, we get
$\dfrac{ar\left( \Delta ABC \right)}{ar\left( \Delta DEF \right)}=9$
The values that can be inculcated through celebration of national festivals are unity of the nation, fraternity and patriotism.
Note: We must remember that we need to find the ratio $\dfrac{ar\left( \Delta ABC \right)}{ar\left( \Delta DEF \right)}$ and not $\dfrac{ar\left( \Delta DEF \right)}{ar\left( \Delta ABC \right)}$. Also, we must take utmost care while writing the corresponding sides, as it is very easy to mistake at this point. We can see that the last part of this question is a value-based question.
Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 7 English: Engaging Questions & Answers for Success

Trending doubts
What are the factors of 100 class 7 maths CBSE

Which are the Top 10 Largest Countries of the World?

What is BLO What is the full form of BLO class 8 social science CBSE

The value of 6 more than 7 is A 1 B 1 C 13 D 13 class 7 maths CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE




