
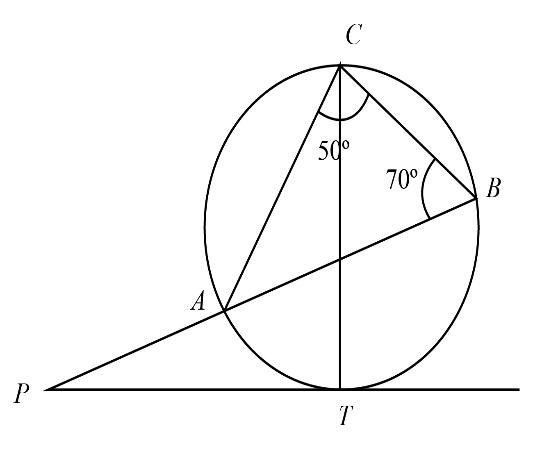
$PT$ is the tangent and $CT$ is the diameter. Find $\angle APT$.

Answer
574.8k+ views
Hint: To find the given angle, we will use the different properties of triangle and circle. We will use the angle sum property of the triangle according to which the sum of all the interior angles of the triangle is always supplementary. Then we will also use the property of the tangent of the circle which states that the angle formed by the tangent and the diameter of the circle will always be right angles. We will do constructions to use the property of the segment of the circle.
Complete step by step answer:
Given: $PT$ is the tangent and $CT$ is the diameter. $\angle ACB = {50^ \circ }$ and $\angle ABC = {70^ \circ }$.
We will consider triangle $\Delta ACB$, such that from the property of the triangle the sum of all the interior will be ${180^ \circ }$ . This can be expressed as:
$\angle ACB + \angle CAB + \angle ABC = {180^ \circ }$
We will substitute the values of $\angle ACB$ and $\angle ABC$ as given in the questions.
$\begin{array}{c}
{50^ \circ } + \angle CAB + {70^ \circ } = {180^ \circ }\\
\angle CAB = {180^ \circ } - {70^ \circ } - {50^ \circ }\\
\angle CAB = {60^ \circ }
\end{array}$
Now, we will join point $T$ and $B$. We know that angle subtended by the diameter on the circumference of the circle is always equal to ${90^ \circ }$ .Therefore,
$\begin{array}{c}
\angle CBT = {90^ \circ }\\
\angle CBO + \angle TBO = {90^ \circ }
\end{array}$
Now we will substitute ${70^ \circ }$ for $\angle CBO$ in the above expression, we get,
$\begin{array}{c}
{70^ \circ } + \angle TBO = {90^ \circ }\\
\angle TBO = {90^ \circ } - {70^ \circ }\\
\angle TBO = {20^ \circ }
\end{array}$
We know that angles formed by the same segment are always equal. Hence we can express it as:
$\begin{array}{l}
\angle TBO = \angle ACO\\
\angle ACO = {20^ \circ }
\end{array}$
Now, we will consider $\Delta AOC$, such that from the property of the triangle the sum of all the interior will be ${180^ \circ }$.
$\angle CAO + \angle ACO + \angle AOC = {180^ \circ }$
We will substitute the values of $\angle CAO$ and $\angle ACO$ as given in the questions.
$\begin{array}{c}
{60^ \circ } + {20^ \circ } + \angle AOC = {180^ \circ }\\
\angle AOC = {180^ \circ } - {60^ \circ } - {20^ \circ }\\
\angle AOC = {100^ \circ }
\end{array}$
Now, we know that $CT$ is the diameter, hence $\angle AOC$ and $\angle AOT$ are linear angles. This can be expressed as:
$\angle AOC + \angle AOT = {180^ \circ }$
We will substitute ${100^ \circ }$for $\angle AOC$ in the above expression.
\[\begin{array}{c}
{100^ \circ } + \angle AOT = {180^ \circ }\\
\angle AOT = {180^ \circ } - {100^ \circ }\\
\angle AOT = {80^ \circ }
\end{array}\]
Now, we will consider $\Delta POT$, such that from the property of the triangle the sum of all the interior will be ${180^ \circ }$.
$\angle AOT + \angle OTP + \angle APT = {180^ \circ }$
We will substitute ${80^ \circ }$for $\angle AOT$ in the above expression. Also, angled formed by the tangent is always equal to ${90^ \circ }$ . Hence e$\angle OTP = {90^ \circ }$.
$\begin{array}{c}
{90^ \circ } + {80^ \circ } + \angle APT = {180^ \circ }\\
\angle APT = {180^ \circ } - {90^ \circ } - {80^ \circ }\\
\angle APT = {10^ \circ }
\end{array}$
Hence, the angle $\angle APT = {10^ \circ }$.
Note: We should have the prior knowledge about the properties of tangent of the circle and also the segments of the circle. Here we are using the angle sum property of triangles to find certain angles. Hence, we should have the prior knowledge of properties of triangles.
Complete step by step answer:
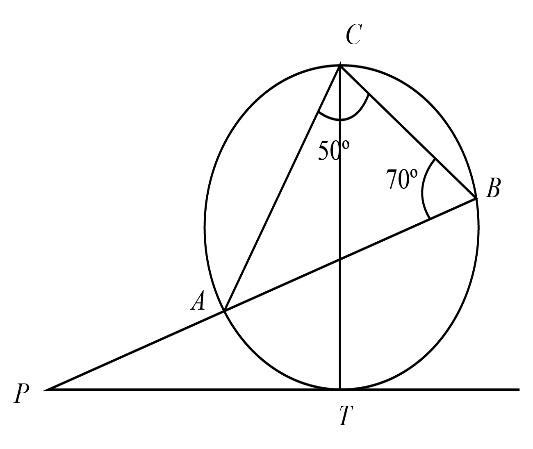
Given: $PT$ is the tangent and $CT$ is the diameter. $\angle ACB = {50^ \circ }$ and $\angle ABC = {70^ \circ }$.

We will consider triangle $\Delta ACB$, such that from the property of the triangle the sum of all the interior will be ${180^ \circ }$ . This can be expressed as:
$\angle ACB + \angle CAB + \angle ABC = {180^ \circ }$
We will substitute the values of $\angle ACB$ and $\angle ABC$ as given in the questions.
$\begin{array}{c}
{50^ \circ } + \angle CAB + {70^ \circ } = {180^ \circ }\\
\angle CAB = {180^ \circ } - {70^ \circ } - {50^ \circ }\\
\angle CAB = {60^ \circ }
\end{array}$
Now, we will join point $T$ and $B$. We know that angle subtended by the diameter on the circumference of the circle is always equal to ${90^ \circ }$ .Therefore,
$\begin{array}{c}
\angle CBT = {90^ \circ }\\
\angle CBO + \angle TBO = {90^ \circ }
\end{array}$
Now we will substitute ${70^ \circ }$ for $\angle CBO$ in the above expression, we get,
$\begin{array}{c}
{70^ \circ } + \angle TBO = {90^ \circ }\\
\angle TBO = {90^ \circ } - {70^ \circ }\\
\angle TBO = {20^ \circ }
\end{array}$
We know that angles formed by the same segment are always equal. Hence we can express it as:
$\begin{array}{l}
\angle TBO = \angle ACO\\
\angle ACO = {20^ \circ }
\end{array}$
Now, we will consider $\Delta AOC$, such that from the property of the triangle the sum of all the interior will be ${180^ \circ }$.
$\angle CAO + \angle ACO + \angle AOC = {180^ \circ }$
We will substitute the values of $\angle CAO$ and $\angle ACO$ as given in the questions.
$\begin{array}{c}
{60^ \circ } + {20^ \circ } + \angle AOC = {180^ \circ }\\
\angle AOC = {180^ \circ } - {60^ \circ } - {20^ \circ }\\
\angle AOC = {100^ \circ }
\end{array}$
Now, we know that $CT$ is the diameter, hence $\angle AOC$ and $\angle AOT$ are linear angles. This can be expressed as:
$\angle AOC + \angle AOT = {180^ \circ }$
We will substitute ${100^ \circ }$for $\angle AOC$ in the above expression.
\[\begin{array}{c}
{100^ \circ } + \angle AOT = {180^ \circ }\\
\angle AOT = {180^ \circ } - {100^ \circ }\\
\angle AOT = {80^ \circ }
\end{array}\]
Now, we will consider $\Delta POT$, such that from the property of the triangle the sum of all the interior will be ${180^ \circ }$.
$\angle AOT + \angle OTP + \angle APT = {180^ \circ }$
We will substitute ${80^ \circ }$for $\angle AOT$ in the above expression. Also, angled formed by the tangent is always equal to ${90^ \circ }$ . Hence e$\angle OTP = {90^ \circ }$.
$\begin{array}{c}
{90^ \circ } + {80^ \circ } + \angle APT = {180^ \circ }\\
\angle APT = {180^ \circ } - {90^ \circ } - {80^ \circ }\\
\angle APT = {10^ \circ }
\end{array}$
Hence, the angle $\angle APT = {10^ \circ }$.
Note: We should have the prior knowledge about the properties of tangent of the circle and also the segments of the circle. Here we are using the angle sum property of triangles to find certain angles. Hence, we should have the prior knowledge of properties of triangles.
Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is pollution? How many types of pollution? Define it

What is the Full Form of ISI and RAW




