Question

Prove theoretically the relation between emf induced in a coil and the rate of change of magnetic flux in electromagnetic induction. A parallel plate air condenser has a capacitor of 20\[\mu F\]. What will the new capacity if:
(a) The distance between the two plates is doubled?
(b) A marble slab of dielectric constant 8 is introduced between the two plates?

Answer 1

Hint: We can easily prove the relation between the induced emf in a coil and the electromagnetic induction by the Faraday’s law of electromagnetic induction. Also, we can find the relation between the distance between the plates and the medium between them in a capacitor.

Complete answer:
According to Faraday's law of electromagnetic induction, the change of magnetic flux with time around a conductor can cause an induced emf in it. i.e., an emf is induced in a conductor which is equal to the rate of change of magnetic flux. This is given by –
\[\varepsilon =-N\dfrac{d{{\phi }_{B}}}{dt}\]
Where, N is the number of turns of the coil used,
\[{{\phi }_{B}}\] is the magnetic flux
\[\varepsilon \]is the induced emf
When a coil is subjected to a change in the magnetic flux with time the coil experiences an induced emf, which it opposes and therefore, the negative symbol.
Now, let us consider a parallel plate capacitor as shown in the figure –
  

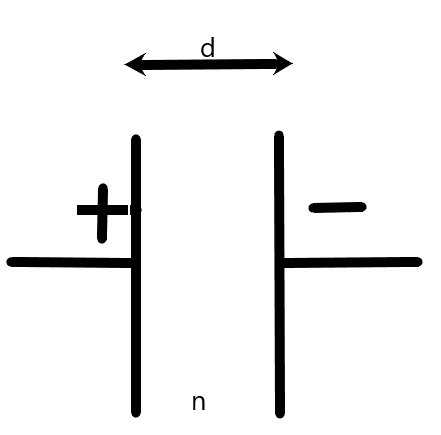
Where, d is the distance between the two plates,
n is the dielectric constant of the medium
We know the capacitance of a parallel plate capacitors is given by –
\[C=\dfrac{{{\varepsilon }_{0}}A}{d}\]
Where A is the area of the plate and
\[{{\varepsilon }_{0}}\] is the dielectric constant of the medium, here air.
(a)The capacitor plates are said to be moved away, or, their distance has been doubled. i.e.,
\[d'=2d\]
So, the capacitance becomes –
\[\begin{align}
  & C'=\dfrac{{{\varepsilon }_{0}}A}{d'} \\
 & \Rightarrow C'=\dfrac{{{\varepsilon }_{0}}A}{2d}=\dfrac{C}{2} \\
\end{align}\]
The capacitance becomes half of the initial condition.
(b) When a medium of dielectric constant 8 is added to the parallel plate capacitor, the permittivity becomes –
\[\begin{align}
  & \varepsilon ={{\varepsilon }_{0}}K \\
 & K=8 \\
 & \Rightarrow \varepsilon =8{{\varepsilon }_{0}} \\
\end{align}\]
The capacitance of the system becomes –
\[C'=\dfrac{8{{\varepsilon }_{0}}A}{d}=8C\]
The capacitance becomes eight times the initial condition.

The required solutions are –
(a) The capacitance becomes half, i.e., 10\[\mu F\].
(b) The capacitance becomes eight times, i.e., 80\[\mu F\].

Note:
The above calculations are based on the assumption that the capacitor is not connected to an external power supply. The value of capacitance will be different if there is a voltage that feeds the plates continuously. So we should be careful with such cases.