Question

Prove the theorem (SAS Similarity Criterion) if in two triangles, one pair of corresponding sides are proportional and the included angles are equal then the two triangles are similar.

Answer 1

Hint: In order to prove the above theorem take two triangles $\vartriangle ABC$ and $\vartriangle DEF$, it is given that included angles are equal $\angle A=\angle D$ and one pair of corresponding sides are proportional $\dfrac{AB}{DE}=\dfrac{AC}{DF}$. Draw $X$ and $Y$on sides $DE\And DF$ which implies that $DX=AB$ and $DY=AC$. By replacing the terms $AB\And AC$ in terms of $DX\And DY$ in proportional equations and by subtracting 1 from it. Replace the terms $DE-DX=XE$ and $DF-DY=YF$ in the above equation and by using the theorem: If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side $\left. XY \right\|EF$, the angles $\angle B=\angle E,\angle C=\angle F$.

Complete step-by-step answer:
Given that, two triangles $\vartriangle ABC$ and $\vartriangle DEF$ such that,
The included angles are equal,
$\Rightarrow \angle A=\angle D$
$\Rightarrow \dfrac{AB}{DE}=\dfrac{AC}{DF}$
To prove:
$\Rightarrow \vartriangle ABC\sim \vartriangle DEF$
Construction:
Draw $X$ and $Y$ on sides $DE\And DF$ such that
$\Rightarrow DX=AB$
And
$\Rightarrow DY=AC$
Respectively and join $XY$

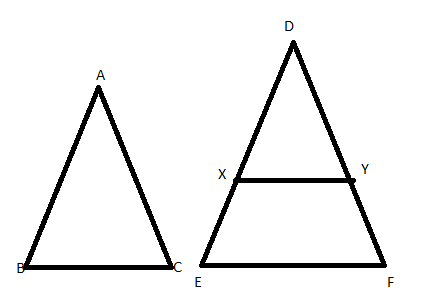
Proof:
Given that,
$\Rightarrow \dfrac{AB}{DE}=\dfrac{CA}{DF}$
And$DX=AB,DY=AC$
$\begin{align}
  & \Rightarrow \dfrac{DX}{DE}=\dfrac{DY}{DF} \\
 & \Rightarrow \dfrac{DE}{DX}=\dfrac{DF}{DY} \\
\end{align}$
Subtracting 1 on both sides,
$\begin{align}
  & \Rightarrow \dfrac{DE}{DX}-1=\dfrac{DF}{DY}-1 \\
 & \Rightarrow \dfrac{DE-DX}{DX}=\dfrac{DF-DY}{DY} \\
\end{align}$
Where, $DE-DX=XE$ and $DF-DY=YF$ applying it on the above equation,
$\Rightarrow \dfrac{XE}{DX}=\frac{YF}{DY}$
$\Rightarrow \dfrac{DX}{XE}=\frac{DY}{YF}$
Using Theorem 6.2: If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
$\Rightarrow \left. XY \right\|EF$
Now,
For lines $XY\And EF$, with transversal $XE$
$\Rightarrow \angle X=\angle E.....(1)$
Corresponding angles
For lines $XY\And EF$, with transversal$YF$
$\Rightarrow \angle Y=\angle F....(2)$
Corresponding angles
Now, in $\vartriangle ABC$ and $\vartriangle DXY$
$\Rightarrow AB=DX$
$\Rightarrow \angle A=\angle D$
$\Rightarrow AC=DY$
$\Rightarrow \vartriangle ABC\cong \vartriangle DXY$
Therefore,
$\begin{align}
  & \Rightarrow \angle B=\angle X \\
 & \Rightarrow \angle C=\angle Y \\
\end{align}$
But from (1) $\angle X=\angle E$ and $\angle Y=\angle F$
Therefore,
$\begin{align}
  & \Rightarrow \angle B=\angle X=\angle E...(3) \\
 & \Rightarrow \angle C=\angle Y=\angle F....(4) \\
\end{align}$
Therefore, in $\vartriangle ABC$ and $\vartriangle DEF$ from equation (3) and (4)
$\begin{align}
  & \Rightarrow \angle B=\angle E \\
 & \Rightarrow \angle C=\angle F \\
\end{align}$
Therefore,
$\Rightarrow \vartriangle ABC\sim \vartriangle DEF$
Hence proved

Note: If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side. For lines $XY\And EF$, with transversal $XE$ $\angle X=\angle E$ and for lines XY and EF, with transversal YF $\angle Y=\angle F$ . In $\vartriangle ABC$ and $\vartriangle DEF$ $\angle B=\angle E$ and $\angle C=\angle F$