Question

Prove the midpoint theorem. In the given triangle $NO\parallel LM$, KN=2.7cm, KL=5.4cm, KO=3.9cm, Find OM.

Answer 1

Hint: Here in this question we will first proof mid-point theorem and with the help of its result further we will solve the numerical part of the question.
Mid-point theorem: - It says a line segment joining the mid-points of two sides of a triangle is parallel to the third side and equal to half the length of the third side.

Complete step-by-step answer:
Draw a $\vartriangle ABC$ where E and F are the mid-points of side AB and AC. Through point ‘C’ draw a line segment parallel to AB and extend EF to meet this line at point ‘D‘
          

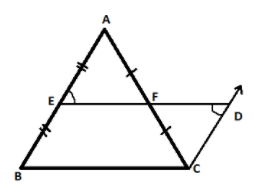
Since $AB\parallel CD$ (by construction) and ED is a transversal line then from the property of parallel lines we can say that
 $\angle AEF = \angle CDF$ (Alternate angles) ...........................equation (1)
In $\vartriangle AEF$ and $\vartriangle CDF$
$\angle AEF = \angle CDF$ (From equation (1))
$\angle AFE = \angle CFD$ (Vertically opposite angle)
$AF = FC$ (As F is the midpoint of AC)
[By AAS (angle angle side) congruence rule]
So, EA=CD (By CPCT)
But EB=EA (Because E is the mid-point of AB)
Therefore EB=CD
Now in EBCD, $EB\parallel DC\& EB = DC$ (Proved above)
Thus one pair of opposite sides is equal and parallel. Hence EBCD is a parallelogram.
Since opposite sides of parallelograms are parallel.
So, $ED\parallel BC$
$\therefore EF\parallel BC$ (As F is a point on line ED)
Thus a mid-point theorem which states that a line segment joining the mid-points of two sides of a triangle is parallel to the third side and equal to half the length of the third side is proved.
Now we will solve another part of the question: -
               

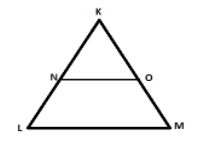
In the given triangle $NO\parallel LM$, KN=2.7cm, KL=5.4cm, KO=3.9cm and we have to find OM.
As $NO\parallel LM$ we can say through mid-point theorem that N and O are the mid-points of side KL and KM
Therefore KN=NL and KO=OM
So, NL=2.7cm and OM=3.9cm
Hence final answer is OM=3.9cm

Note: Students may likely make mistakes while applying the mid-point theorem they should be cautious about which sides are parallel and which points are mid-points related to these parallel sides.