Question

Prove the following theorem.
Converse of Pythagoras’ Theorem: In a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then the angle opposite to the first side is a right angle.

Answer 1

Hint: Here, draw the triangle given and draw another triangle similar to the given triangle. Then compare the two triangles and using similarity properties, prove the theorem asked in question.

Complete step-by-step answer:
Given: A ∆ABC in which \[A{C^2} = A{B^2} + B{C^2}\]
To prove: ∠B = 90°
Construction: Draw a ∆DEF such that DE = AB, EF = BC and ∠E = 90°.

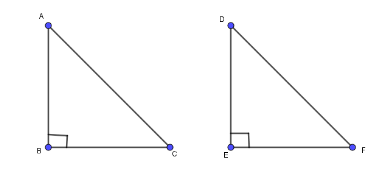
Proof: In ∆DEF, we have: ∠E = 90°
So, by Pythagoras theorem, we have
\[D{F^2} = D{E^2} + E{F^2}\]
\[D{F^2} = A{B^2} + B{C^2}\] ...(i) [Since, DE = AB and EF = BC]
But \[A{C^2} = A{B^2} + B{C^2}\] ...(ii) [Given]
From (i) and (ii), we get
\[\Rightarrow A{C^2} = D{F^2}\] ⇒ AC = DF
Now, in ∆ABC and ∆DEF, we have
AB = DE, BC = EF and AC = DF
∴ ∆ABC ≅ ∆DEF [By SSS congruence criteria]
[SSS congruence criteria states that if corresponding sides of two triangles are proportional then their corresponding angles are equal, and hence the two triangles are similar.]
Hence, ∠B = ∠E = 90°.

Note: In these types of questions, use the concept of similarity of triangles. Use different types of congruence criteria to compare two triangles whether congruent or not.
Two triangles are said to be congruent if all sides and all angles of one triangle are equal to all sides and all angles of another triangle.
Also, there I difference between similar triangles and congruent triangles.
Some important definitions about similar triangles:
(AAA-similarity): If in two triangles, the corresponding angles are equal, then their corresponding sides are proportional and hence the triangles are similar.