Question

Prove that the two lines that are respectively perpendicular to two intersecting lines intersect each other.

Answer 1

Hint: We will assume two lines P and Q intersecting each other and L and M as the lines perpendicular to each other. We will then assume that $L\parallel M$ and if our assumption goes correct then L is actually parallel to M and if our assumption goes wrong, then it will show that L will intersect M at some point.

Complete step-by-step answer:
It is given in the question, to prove that the two lines that are respectively perpendicular to two intersecting lines intersect each other. Let us assume that P and Q are two intersecting lines. We will also assume that L is perpendicular to Q and M is perpendicular to P. So, we can represent it as follows.

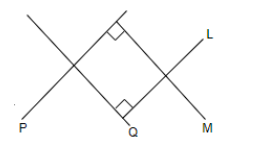
Now, we have to prove that L and M will intersect at some point. We already know that P and Q are two intersecting lines. We will assume that the perpendicular lines L and M do not intersect each other, but they are parallel to each other, that is, $L\parallel M$ (assumption) ……… (i)
Now, we had assumed initially that L is perpendicular to Q, that is, $L\bot Q.........\left( ii \right)$. Also, we had assumed that M is perpendicular to P, that is, $M\bot P.........\left( iii \right)$.
So, from equations (i), (ii) and (iii), we can say that if $L\parallel M$, then P must be parallel to Q. But, we know that P and Q are intersecting lines and will contradict our assumption that L and M are parallel lines, it means that L and M will intersect each other.
Therefore, the lines L and M will intersect each other at a point.

Note: Many times the students make mistakes in understanding the question, they may understand the question as P and Q are the intersecting lines and they intersect perpendicularly, which results in the wrong answer. Hence, it is recommended that the students read the question carefully.