
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Answer
528.3k+ views
Hint: Divide the given each triangle into two half and use congruence properties and CPCT (corresponding parts of congruent triangles)
Since the median divides the triangles into another two triangles and the base of triangle into equal two halves from which we get an equation or an expression from both the triangle and then using CPCT, we will be able to prove the required statement
Complete step by step solution:
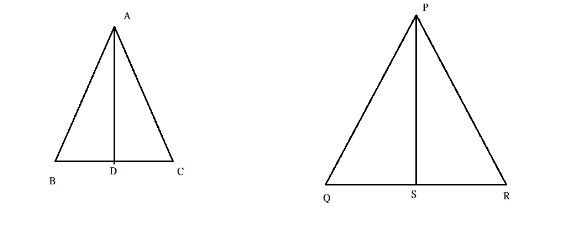
Consider the above diagram for proving the required statement
GIVEN:
We, given that the two triangles are similar, it means that
$ \vartriangle ABC \sim \vartriangle PQR $ .
So, we know that there are medians for each of the triangles.
So, for the $ \vartriangle ABC $ , AD is the median. It means that
$ BD = CD = \dfrac{1}{2}BC $ ----------(1)
Similarly, for the $ \vartriangle PQR $ , PS is the median. It means that
$ QS = RS = \dfrac{1}{2}QR $ ------------(2)
REQUIRED TO PROVE: $ \dfrac{{ar(\vartriangle ABC)}}{{ar\left( {\vartriangle PQR} \right)}} = {\left( {\dfrac{{AD}}{{PS}}} \right)^2} $
PROOF:
We are given that $ \vartriangle ABC \sim \vartriangle PQR $
So,
$ \angle B = \angle Q $
Since, corresponding angles of similar triangles are equal.
So, by using corresponding sides of similar triangles, we will get
$ \dfrac{{AB}}{{PQ}} = \dfrac{{BC}}{{QR}} $
From (1) and (2), we will get
$
\dfrac{{AB}}{{PQ}} = \dfrac{{2BD}}{{2QS}} \\
\dfrac{{AB}}{{PQ}} = \dfrac{{BD}}{{QS}} \\
$ ---------------(3)
In $ \vartriangle ABD\,\,and\,\,\vartriangle PQS $
We know that $ \angle B = \angle Q $
And also
$ \dfrac{{AB}}{{PQ}} = \dfrac{{BD}}{{QS}} $
Therefore $ \vartriangle ABD \sim \vartriangle PQS $ by SAS similarity.
From this we will get using CPCT
$ \dfrac{{AB}}{{PQ}} = \dfrac{{AD}}{{PS}} $ -----------(4)
Since, we know that $ \vartriangle ABC \sim \vartriangle PQR $
It means that the ratio of their area is equal to the square of their corresponding sides. It means that
$ \dfrac{{ar(\vartriangle ABC)}}{{ar\left( {\vartriangle PQR} \right)}} = {\left( {\dfrac{{AB}}{{PQ}}} \right)^2} $
From the equation (4), we get
$ \dfrac{{ar(\vartriangle ABC)}}{{ar\left( {\vartriangle PQR} \right)}} = {\left( {\dfrac{{AD}}{{PS}}} \right)^2} $
Hence proved.
Note: While solving the problem, we have to be careful while choosing the corresponding sides as we are forming equations for the later purpose, if there is an error done, then we cannot derive what is asked and required in the question.
Since the median divides the triangles into another two triangles and the base of triangle into equal two halves from which we get an equation or an expression from both the triangle and then using CPCT, we will be able to prove the required statement
Complete step by step solution:
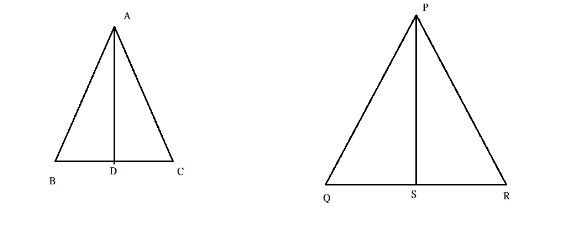
Consider the above diagram for proving the required statement
GIVEN:
We, given that the two triangles are similar, it means that
$ \vartriangle ABC \sim \vartriangle PQR $ .
So, we know that there are medians for each of the triangles.
So, for the $ \vartriangle ABC $ , AD is the median. It means that
$ BD = CD = \dfrac{1}{2}BC $ ----------(1)
Similarly, for the $ \vartriangle PQR $ , PS is the median. It means that
$ QS = RS = \dfrac{1}{2}QR $ ------------(2)
REQUIRED TO PROVE: $ \dfrac{{ar(\vartriangle ABC)}}{{ar\left( {\vartriangle PQR} \right)}} = {\left( {\dfrac{{AD}}{{PS}}} \right)^2} $
PROOF:
We are given that $ \vartriangle ABC \sim \vartriangle PQR $
So,
$ \angle B = \angle Q $
Since, corresponding angles of similar triangles are equal.
So, by using corresponding sides of similar triangles, we will get
$ \dfrac{{AB}}{{PQ}} = \dfrac{{BC}}{{QR}} $
From (1) and (2), we will get
$
\dfrac{{AB}}{{PQ}} = \dfrac{{2BD}}{{2QS}} \\
\dfrac{{AB}}{{PQ}} = \dfrac{{BD}}{{QS}} \\
$ ---------------(3)
In $ \vartriangle ABD\,\,and\,\,\vartriangle PQS $
We know that $ \angle B = \angle Q $
And also
$ \dfrac{{AB}}{{PQ}} = \dfrac{{BD}}{{QS}} $
Therefore $ \vartriangle ABD \sim \vartriangle PQS $ by SAS similarity.
From this we will get using CPCT
$ \dfrac{{AB}}{{PQ}} = \dfrac{{AD}}{{PS}} $ -----------(4)
Since, we know that $ \vartriangle ABC \sim \vartriangle PQR $
It means that the ratio of their area is equal to the square of their corresponding sides. It means that
$ \dfrac{{ar(\vartriangle ABC)}}{{ar\left( {\vartriangle PQR} \right)}} = {\left( {\dfrac{{AB}}{{PQ}}} \right)^2} $
From the equation (4), we get
$ \dfrac{{ar(\vartriangle ABC)}}{{ar\left( {\vartriangle PQR} \right)}} = {\left( {\dfrac{{AD}}{{PS}}} \right)^2} $
Hence proved.
Note: While solving the problem, we have to be careful while choosing the corresponding sides as we are forming equations for the later purpose, if there is an error done, then we cannot derive what is asked and required in the question.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is pollution? How many types of pollution? Define it

What is the Full Form of ISI and RAW




