Question

Prove that the locus of intersection of normal at the ends of conjugate diameter is the curve \[2{{\left( {{a}^{2}}{{x}^{2}}+{{b}^{2}}{{y}^{2}} \right)}^{3}}={{\left( {{a}^{2}}-{{b}^{2}} \right)}^{2}}{{\left( {{a}^{2}}{{x}^{2}}-{{b}^{2}}{{y}^{2}} \right)}^{2}}\].

Answer 1

Hint: Use the concept of conjugate diameters i.e. \[\theta -\varphi =\pm \dfrac{\pi }{2}\]where \[\theta \And \varphi \]are eccentric angles of points of conjugate diameter. Write down the equations of normal and eliminate (\[\theta \And \varphi \]) parametric angles.

Complete answer: Let us first suppose CP and CD are two conjugate diameters.
 

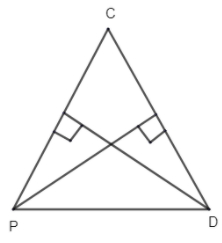
Here we can see that tangent through P is parallel to CD and tangent through D is parallel to PC. Hence, normal to P point is perpendicular to CD and normal to D is perpendicular to PC. Hence, in other words we need to find the orthocentre of \[\vartriangle CPD\]or intersections of normal.
We have given ellipse; \[\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1-(1)\]
Here, we need to assume points of conjugate diameters.
Let \[\varphi \]is the eccentric angle of point P, then coordinates of \[P=\left( a\cos \varphi ,b\sin \varphi \right)\].
  

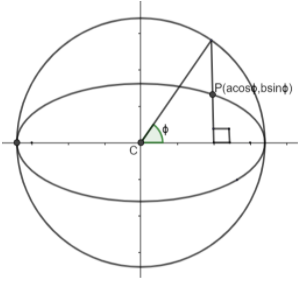
Eccentric angle is the angle between the major axis and line joining the circle at a point where perpendicular from any point to the major axis ellipse is extended to the circle as shown in diagram.
Since CP and CD are conjugate diameters. Hence, tangent at P is parallel to CD as per the definition of conjugate diameter.
Imp point: -
1. We need to know the relation between the two conjugate diameters i.e. If \[\left( a\cos \theta ,b\sin \theta \right)\]be the coordinates of the extremity of a diameter then \[\left( -a\sin \theta ,b\cos \theta \right)\]will be the coordinates of the extremity of its conjugate.
It means \[\theta -\varphi =\pm \dfrac{\pi }{2}\].
If \[\theta \] is an eccentric angle for extremity of a diameter and \[\varphi \] is eccentric angle of extremity of other diameter.
Hence, \[\vartriangle CPD\] can be represented as

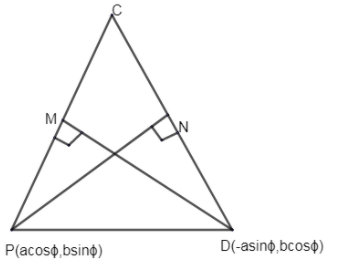
Since, C, P, D are on a circle and \[PM\bot CD\], where CD is parallel to the tangent at point P; Hence PM is normal at point P.
Similarly, DN is normal at point D.
Hence, equations of both normal PM & DN respectively are: -
\[ax\sec \varphi -by\cos ec\varphi ={{a}^{2}}-{{b}^{2}}-(2)\]
(Standard formula for normal through \[a\sin \varphi ,b\cos \varphi \])
\[-ax\cos ec-by\sec \varphi ={{a}^{2}}-{{b}^{2}}-(3)\]
The locus of the orthocentre of \[\vartriangle CPD\]is obtained by eliminating \[\varphi \]between (2) and (3)
Apply cross multiplication in following manner: -
\[\dfrac{\sec \varphi }{\left( by-ax \right)\left( {{a}^{2}}-{{b}^{2}} \right)}=\dfrac{\cos ec\varphi }{\left( by+ax \right)\left( {{a}^{2}}-{{b}^{2}} \right)}=\dfrac{-1}{\left( {{b}^{2}}{{y}^{2}}+{{a}^{2}}{{x}^{2}} \right)}\]
From the above equation we can write
\[\begin{align}
  & \sec \varphi =\dfrac{\left( by-ax \right)\left( {{a}^{2}}-{{b}^{2}} \right)}{-\left( {{b}^{2}}{{y}^{2}}+{{a}^{2}}{{x}^{2}} \right)} \\
 & \cos ec\varphi =\dfrac{\left( by+ax \right)\left( {{a}^{2}}-{{b}^{2}} \right)}{-\left( {{b}^{2}}{{y}^{2}}+{{a}^{2}}{{x}^{2}} \right)} \\
\end{align}\]
As we know the relation \[{{\sin }^{2}}\varphi +{{\cos }^{2}}\varphi =1\]
\[\begin{align}
  & 1=\dfrac{{{\left( {{b}^{2}}{{y}^{2}}+{{a}^{2}}{{x}^{2}} \right)}^{2}}}{{{\left( by-ax \right)}^{2}}{{\left( {{a}^{2}}-{{b}^{2}} \right)}^{2}}}+\dfrac{{{\left( {{b}^{2}}{{y}^{2}}+{{a}^{2}}{{x}^{2}} \right)}^{2}}}{{{\left( by+ax \right)}^{2}}{{\left( {{a}^{2}}-{{b}^{2}} \right)}^{2}}} \\
 & \dfrac{{{\left( {{b}^{2}}{{y}^{2}}+{{a}^{2}}{{x}^{2}} \right)}^{2}}}{{{\left( {{a}^{2}}-{{b}^{2}} \right)}^{2}}}\left( \dfrac{1}{{{\left( by-ax \right)}^{2}}}+\dfrac{1}{{{\left( by+ax \right)}^{2}}} \right)=1 \\
 & \dfrac{{{\left( {{b}^{2}}{{y}^{2}}+{{a}^{2}}{{x}^{2}} \right)}^{2}}}{{{\left( {{a}^{2}}-{{b}^{2}} \right)}^{2}}}\times \dfrac{{{\left( by-ax \right)}^{2}}+{{\left( by+ax \right)}^{2}}}{{{\left( {{b}^{2}}{{y}^{2}}-{{a}^{2}}{{x}^{2}} \right)}^{2}}}=1 \\
 & 2{{\left( {{b}^{2}}{{y}^{2}}+{{a}^{2}}{{x}^{2}} \right)}^{3}}={{\left( {{a}^{2}}-{{b}^{2}} \right)}^{2}}{{\left( {{b}^{2}}{{y}^{2}}-{{a}^{2}}{{x}^{2}} \right)}^{2}} \\
\end{align}\]
Hence proved.

Note:
Terms like auxiliary circle, eccentric angle, orthocentre, conjugate diameters & relation between conjugate diameters should be clearly known otherwise it may take a very long time to solve.
Calculation part is also an important one.