Question

Prove that the line of centers of two intersecting circles subtends equal angles at the two points of intersection

Answer 1

Hint: A circle consists of a center point that can be taken as reference to draw the radius, diameter and any chord in it. It is given that two circles intersecting that means the two circles will overlap at any two points. So name the intersecting points and observe the circles to prove the given statement.

Complete step-by-step answer:
The following is the schematic diagram of two intersecting circles in which join the points PQ, PR, PS, QR, and QS.

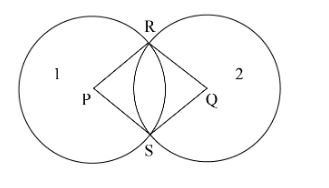
As per the diagram, we can observe that, C and D are the intersecting points of the two circles. Then we can say that,
The radius of the 1st circle is PR or PS and the radius of the 2nd circle is QR or QS.
According to the construction, we can observe that two triangles were formed, they are \[\Delta PRQ\] and \[\Delta PSQ\].The sides PR is equal to QR because PR and QR are radius of the two circles and similarly PS is equal to QS because PS and QS are radius of the two circles.
\[\begin{array}{l}
PR = QR\\
PS = QS
\end{array}\]
 Also, we know that PQ is the common side or base of the two triangles \[\Delta PRQ\] and \[\Delta PSQ\].
So, according to the SSS (Side Side Side) congruency, it can be said that two intersecting circles subtends equal angles at the two points of intersection if all sides are congruent to each other.
Therefore, the line of centers of two intersecting circles subtends equal angles at the two points of intersection. Hence proved.

Note: Make sure and aware about the congruency rules in the triangle because after joining the all points we can observe two triangles in the circle, so according to the congruence rule we can prove the given statement without any angle.