Question

Prove that the length of the common chord of the circles \[{{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{c}^{2}}\] and \[{{\left( x-b \right)}^{2}}+{{\left( y-a \right)}^{2}}={{c}^{2}}\] is \[\sqrt{4{{c}^{2}}-2{{\left( a-b \right)}^{2}}}\]. Hence find the condition that the two circles touch each other.

Answer 1

Hint: To solve this question, we should have a little bit of knowledge of coordinate geometry like distance formula, that is the distance between two points \[\left( {{x}_{1}},{{y}_{1}} \right)\] and \[\left( {{x}_{2}},{{y}_{2}} \right)\] is given by \[\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]. Also, we should know the concept of the Pythagoras Theorem. By using these formulas, we will be able to prove the required result.

Complete step-by-step answer:
In this question, we have to prove that the length of the common chord of the circles \[{{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{c}^{2}}\] and \[{{\left( x-b \right)}^{2}}+{{\left( y-a \right)}^{2}}={{c}^{2}}\] is \[\sqrt{4{{c}^{2}}-2{{\left( a-b \right)}^{2}}}\]. We can draw the figure of the given condition as:

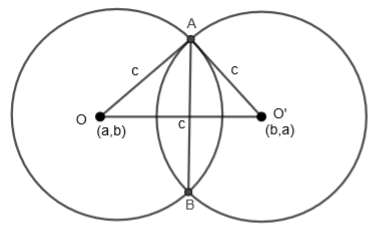
Here, the circle with center O represents \[{{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{c}^{2}}\] and circle with center O’ represents \[{{\left( x-b \right)}^{2}}+{{\left( y-a \right)}^{2}}={{c}^{2}}\]. And from the equation, we can see that O is at (a, b) and O’ at (b, a). Also, we can see that the radius of both the circle is C. Now, we will apply distance formula for O (a, b) and O’ (b, a), that is \[\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\]. So, we get,
\[OO'=\sqrt{{{\left( a-b \right)}^{2}}+{{\left( b-a \right)}^{2}}}\]
\[OO'=\sqrt{{{\left( a-b \right)}^{2}}+{{\left( a-b \right)}^{2}}}\]
\[OO'=\sqrt{2}\sqrt{{{\left( a-b \right)}^{2}}}\]
\[OO'=\sqrt{2}\left| a-b \right|\]
We have been given that both the circles are of equal radii. So, the common chord will be the perpendicular bisector of the line joining centers of the circle. Therefore, we can write,
\[OO'=2OC\]
\[OC=\dfrac{OO'}{2}\]
Now, we will put the value of OO’. So, we get,
\[OC=\dfrac{\sqrt{2}\left| a-b \right|}{2}\]
\[OC=\dfrac{\left| a-b \right|}{\sqrt{2}}\]
Now, in \[\Delta AOC\], we will apply the Pythagoras theorem. So, we will get,
\[{{\left( AC \right)}^{2}}+{{\left( OC \right)}^{2}}={{\left( AO \right)}^{2}}\]
\[{{\left( AC \right)}^{2}}={{\left( AO \right)}^{2}}-{{\left( OC \right)}^{2}}\]
We can see that AO is nothing but the radius of the circle with center O. So, we can write,
\[{{\left( AC \right)}^{2}}={{c}^{2}}-{{\left( \dfrac{\left| a-b \right|}{\sqrt{2}} \right)}^{2}}\]
\[{{\left( AC \right)}^{2}}={{c}^{2}}-\dfrac{{{\left( a-b \right)}^{2}}}{2}\]
\[{{\left( AC \right)}^{2}}=\dfrac{2{{c}^{2}}-{{\left( a-b \right)}^{2}}}{2}\]
\[AC=\sqrt{\dfrac{2{{c}^{2}}-{{\left( a-b \right)}^{2}}}{2}}\]
Now, we will multiply the numerator and denominator of the equation by 2. So, we will get,
\[AC=\sqrt{\dfrac{4{{c}^{2}}-2{{\left( a-b \right)}^{2}}}{4}}\]
\[AC=\dfrac{\sqrt{4{{c}^{2}}-2{{\left( a-b \right)}^{2}}}}{2}\]
And we know that AC is half of AB. So, we can write
\[AB=2AC\]
Now, we will put the value of AC. So, we will get
\[AB=2\left[ \dfrac{\sqrt{4{{c}^{2}}-2{{\left( a-b \right)}^{2}}}}{2} \right]\]
\[AB=\sqrt{4{{c}^{2}}-2{{\left( a-b \right)}^{2}}}\]
And according to the figure, AB is the length of the common chord. Hence, we have proved that the common chord of the circles \[{{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{c}^{2}}\] and \[{{\left( x-b \right)}^{2}}+{{\left( y-a \right)}^{2}}={{c}^{2}}\] is \[\sqrt{4{{c}^{2}}-2{{\left( a-b \right)}^{2}}}\]. Now, we have to find the condition for which the circle only touches each other. And, we know that if the circle only touches each other, then the length of the common chord is equal to 0. So, we can write,
\[AB=\sqrt{4{{c}^{2}}-2{{\left( a-b \right)}^{2}}}=0\]
\[4{{c}^{2}}-2{{\left( a-b \right)}^{2}}=0\]
\[4{{c}^{2}}=2{{\left( a-b \right)}^{2}}\]
\[{{c}^{2}}=\dfrac{{{\left( a-b \right)}^{2}}}{2}\]
Now, we take the square root to both sides of the equation. So, we will get,
\[c=\dfrac{\left| a-b \right|}{\sqrt{2}}\]
\[c=OC\]
Therefore, the condition for the circles to touch is
\[c=\dfrac{\left| a-b \right|}{\sqrt{2}}=OC\]

Note: In a hurry, the possible mistake one can do is by not solving the second part of the question. It is not at all tough. But we have to remember that when the circle only touches each other, then the length of their common chord is O. And also have to remember the general equation of circle and formula of distance between any two points.