Question

Prove that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is \[\dfrac{{2R}}{{\sqrt 3 }}\]. Also find the maximum volume.

Answer 1

Hint – In this question let the diameter of the base of the cylinder be x units, then apply Pythagoras theorem in triangle DBC to find the relation between x, h and R. Use the direct formula for volume of cylinder and substitute the relationship obtained. Differentiate the volume with respect to height and put it equal to 0, to get the value of h in terms of R.

Complete step-by-step answer:

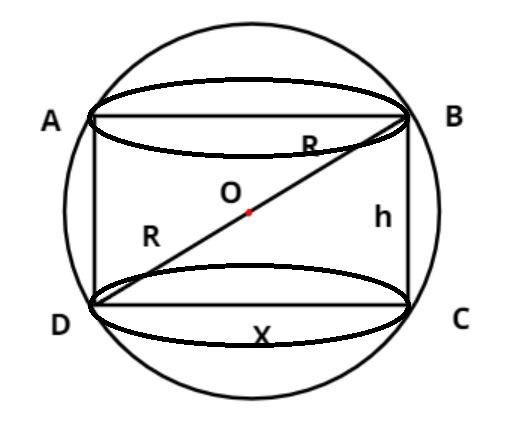
Sphere having the cylinder inscribed is shown in the above figure.
Let the diameter of the base of the cylinder = X unit.
It is given that the radius of the cylinder is = R unit.
So the diameter of the cylinder = twice the radius = 2R unit.
Let the height of the cylinder = h unit.
So applying Pythagoras theorem in triangle DBC we have,
$ \Rightarrow {\left( {{\text{hypotenuse}}} \right)^2} = {\left( {{\text{perpendicular}}} \right)^2} + {\left( {{\text{base}}} \right)^2}$
Now from figure, hypotenuse = 2R, perpendicular = h and base = X.
Now substitute the values we have,
$ \Rightarrow {\left( {2R} \right)^2} = {\left( h \right)^2} + {\left( X \right)^2}$
$ \Rightarrow {X^2} = 4{R^2} - {h^2}$........................ (1)
Now as we know that the volume (V) of the cylinder having base X and height h is given as $V = \pi \times radiu{s^2} \times h$
$ \Rightarrow V = \pi {\left( {\dfrac{X}{2}} \right)^2}h$, [as the radius of the cylinder is half of the base of the cylinder].
Now from equation (1) substitute the value of ${X^2}$ in above equation we have,
$ \Rightarrow V = \pi \left( {\dfrac{{4{R^2} - {h^2}}}{4}} \right)h$
$ \Rightarrow V = \pi {R^2}h - \dfrac{1}{4}\pi {h^3}$........... (2)
Now we have to maximize the volume of the cylinder w.r.t. the height of the cylinder.
So differentiate the above equation w.r.t. h and equate to zero we have,
 $ \Rightarrow \dfrac{d}{{dh}}V = \dfrac{d}{{dh}}\left( {\pi {R^2}h - \dfrac{1}{4}\pi {h^3}} \right) = 0$
Now differentiate it according to the property $\dfrac{d}{{dx}}{x^n} = n{x^{n - 1}}$ we have,
$ \Rightarrow \left( {\pi {R^2} - \dfrac{1}{4}\pi \times 3{h^2}} \right) = 0$
$ \Rightarrow 3\pi {h^2} = 4\pi {R^2}$
$ \Rightarrow {h^2} = \dfrac{4}{3}{R^2}$
Now take square root on both sides we have,
$ \Rightarrow h = \sqrt {\dfrac{4}{3}{R^2}} = \dfrac{{2R}}{{\sqrt 3 }}$
Now double differentiate the equation (2) so that we can conclude whether at this height the volume is maximum or minimum, is $\dfrac{{{d^2}}}{{d{h^2}}}V$= negative than the volume is maximum and if positive then the volume is minimum.
$ \Rightarrow \dfrac{{{d^2}}}{{d{h^2}}}V = \dfrac{{{d^2}}}{{d{h^2}}}\left( {\pi {R^2}h - \dfrac{1}{4}\pi {h^3}} \right) = \dfrac{d}{{dh}}\left( {\pi {R^2} - \dfrac{1}{4}\pi \times 3{h^2}} \right) = - \dfrac{1}{4}\pi \times 6h = \dfrac{{ - 3}}{2}\pi h$
So as we see that h is positive so the double differentiation of the volume is negative so the volume of the cylinder inscribed in the sphere is maximum.
Hence, \[h = \dfrac{{2R}}{{\sqrt 3 }}\] units.
Hence proved.
Now in equation (2) substitute the value of h we have,
$ \Rightarrow V = \pi {R^2}\dfrac{{2R}}{{\sqrt 3 }} - \dfrac{1}{4}\pi {\left( {\dfrac{{2R}}{{\sqrt 3 }}} \right)^3}$
Now simplify this we have,
$ \Rightarrow V = \dfrac{{2\pi {R^3}}}{{\sqrt 3 }} - \dfrac{{2\pi {R^3}}}{{3\sqrt 3 }} = \dfrac{{4\pi {R^3}}}{{3\sqrt 3 }}$ Cubic units.
So this is the required volume.

Note – After putting the first derivative equal to zero, always check the second derivative, if the second derivative with the substitution the value obtained before comes out to be negative that we can say that the value corresponds to the maxima and if it is negative then the value obtained corresponds to minima.