Question

Prove that the equal chords of two congruent circles subtend equal angles at their respective centres.

Answer 1

Hint: Use the fact that the radii of two congruent circles are equal and hence prove that OA = O’A’ and OB = O’B’. Use the fact that since the chords are equal AB = A’B’ and hence prove that the triangle ABC and A’B’C’ are congruent and hence prove that $\angle AOC=\angle A'O'C'$. Hence prove that the equal chords of congruent circles subtend equal angles at the centres of their corresponding circles.

Complete step by step answer:

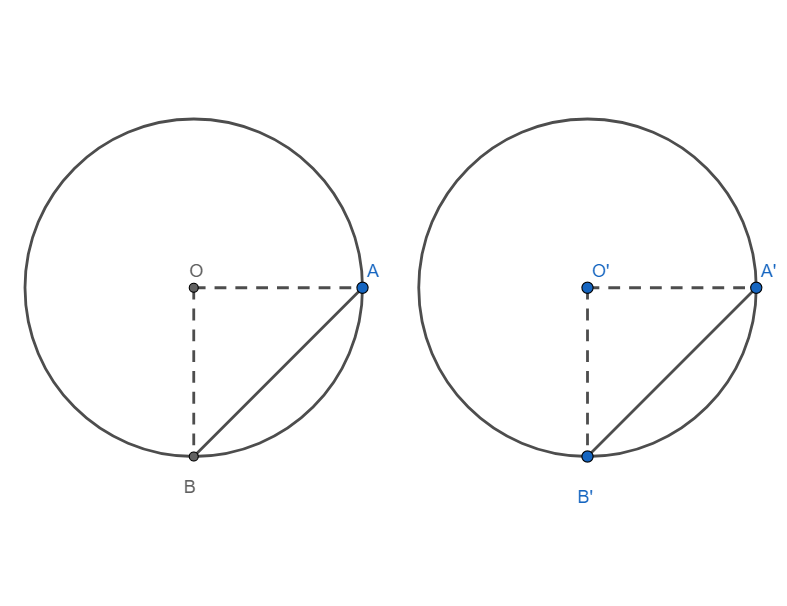
Given: Two circles with centre O and O’ have equal radii. AB is the chord of the circle with centre O and A’B’ is a chord of the circle with centre O’.
To prove $\angle AOB=\angle A'O'B'$
Proof:
Since the circle have equal radii, we have
OA = O’A’ and OB = O’B’
Now, in triangle AOB and A’O’B’, we have
AO = A’O’ (proved above)
OB = O’B’ (Proved above)
AB = A’B’ (Given).
Hence by S.S.S congruence criterion, we have
$\Delta AOB\cong \Delta A'O'B'$
Hence, we have
$\angle AOB=\angle A'O'B'$ (Corresponding parts of congruent triangles)
Hence, equal chords of two congruent circles subtend equal angles at their respective centres.
Hence, proved.

Note: Alternative Solution: Using Sine rule.
We know that if R is the radius of circumcentre of a triangle ABC, then $\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R$

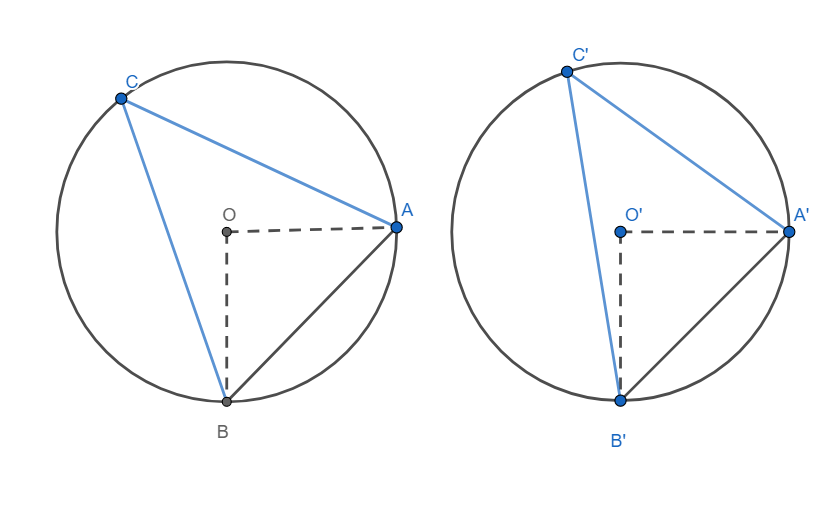
Consider two points C and C’ on the alternate segments as shown in the diagram above.
By sine rule, we have
$\begin{align}
  & \dfrac{AB}{\sin C}=2R \\
 & \Rightarrow AB=2R\sin C \\
\end{align}$
Similarly, we have
$A'B'=2R\sin C'$
Since AB = A’B’, we have
$\begin{align}
  & 2R\sin C=2R\sin C' \\
 & \Rightarrow \sin C=\sin C' \\
 & \Rightarrow C=C' \\
\end{align}$
We know that the angle subtended in the alternate segment is half the angle subtended at the centre.
Hence, we have
$\angle AOB=2\angle C$ and $\angle A'O'B'=2\angle C'$
Since $\angle C=\angle C'$, we have
$\angle AOB=\angle A'O'B'$
Q.E.D