Question

Prove that the distance between the circumcenter and the incenter of the triangle ABC is $\sqrt {{R^2} - 2Rr} $.

Answer 1

Hint: This is a theorem called Euler’s theorem. First we need to prove that triangle ADI and triangle MBL are similar, then we need to prove that $\angle IBL = \angle BIL$ and by using this we will prove this theorem.

Complete step-by-step answer:
Representing the triangle ABC with its circumcenter and incenter in below diagram,

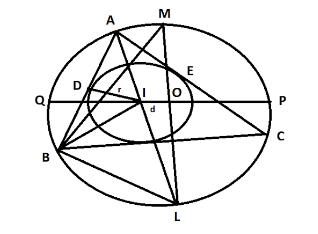
Let O be the circumcenter of triangle ABC and I be the incenter of it.
Ray AI intersects the circumcircle at L.
Ray LO intersects the circumcircle at M.
ID is perpendicular to AB.
ID=r, r be the radius of incircle
IO=d, d be the distance between O and I
OQ = OL = OM = OP = OQ = R, R be the radius of circumcircle
Let \[\angle A = \alpha ,\angle B = \beta \]
In triangle ADI and triangle MBL,
$\angle ADI = \angle MBL = 90^\circ $ and $\angle DAI = \angle BML$(they lie on same cord)
Hence both the triangles are similar.
So, ID/BL = AI/ML
By cross multiplication, $ID \times ML = AI \times BL$
Therefore, $AI \times BL = 2Rr$……………….1
Because, ID= r
And ML= diameter of circumcircle =2R
From the figure, Again, $\angle BIL = \dfrac{{\angle A}}{2} + \dfrac{{\angle B}}{2} = \dfrac{\alpha }{2} + \dfrac{\beta }{2}$
And $\angle IBL = \dfrac{{\angle A}}{2} + \dfrac{{\angle B}}{2} = \dfrac{\alpha }{2} + \dfrac{\beta }{2}$
Hence, $\angle IBL = \angle BIL$
So, IL=BL
From equation 1 we have,
$AI \times BL = 2Rr$
As OI intersects circumcircle on both the sides at P and Q then,
$PI \times QI = AI \times BL = 2Rr$………….2
The distance PI=R+d
The distance QI=R-d
Putting this in equation 2 we get,
(R+d) (R-d)= 2Rr
Solving the above equation we get,
${R^2} - {d^2} = 2Rr$
Putting radius terms in one side,
${d^2} = {R^2} - 2Rr$
Taking square root of above equation,
$d = \sqrt {{R^2} - 2Rr} $
Hence it is proved that the distance between the circumcenter and the incenter of the triangle ABC is $\sqrt {{R^2} - 2Rr} $.

Note: Be cautious while doing the diagram, while measuring and comparing the angles and while comparing the similarity in triangles.
Circumcircle of a triangle is the circle which passes through all the vertices of it and its center is called the circumcenter. Hence all the vertices of the triangle are equidistant from the center of the circle.
Incircle of a triangle is the circle which touches all the sides of the triangle and its center is called incenter.
The area of the triangle can be obtained by multiplying half of the triangle’s perimeter with radius of incircle.