Question

Prove that the angles opposite to equal sides of an isosceles triangle are equal.

Answer 1

Hint: Isosceles triangle in geometry is defined as a triangle whose two sides are of equal length. So, we will use the property of triangles here i.e., by using congruency of the triangle, we will show that angles opposite to equal sides are also equal.

Complete step-by-step answer:
First, let us draw an isosceles triangle.

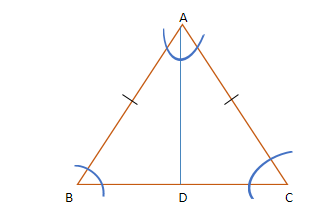
Let us suppose this triangle ABC has sides AB and AC are equal i.e.,
AB= AC
We are required to prove that $\angle B = \angle C$.
For this we will do a bit of construction in the triangle ABC.
We will draw an angle bisector of $\angle A$ which intersects the side BC of the triangle at any point D(say). This means that $\angle A$ has been bisected equally in two parts.
Now, we can see that the triangle ABC is now divided into two triangles namely $\vartriangle ABD$ and $\vartriangle ACD$.
We will prove both of these triangles congruent. For this,
In $\vartriangle ABD$ and $\vartriangle ACD$,
AB = AC (given)
$\angle BAD = \angle CAD$ (as D is the angle bisector of A)
AD = AD (common)
$\therefore \vartriangle ABD \cong \vartriangle ACD$ (by SAS congruency)
Therefore, we have proved that $\vartriangle ABD$and $\vartriangle ACD$are congruent to each other by Side Angle Side Congruence rule.
By corresponding parts of congruent triangles’ rule (CPCT), we get
$
  \angle ABD = \angle ACD \\
   \Rightarrow \angle B = \angle C \\
 $
Hence, it is proved that the angles opposite to equal sides are also equal.


Note: In such types of questions where we are required to prove some theorem, we firstly draw a figure to get a clear idea of what the question is about. Many get confused about how to proceed with. After drawing figure use congruence property of triangle to prove desired result