Question

Prove that tangent segments drawn from an external point to a circle are congruent.

Answer 1

Hint: Here we will be using the given information for forming the figure based on that. Then we will be finding the logical solution to prove the proposition by using the properties of the congruent part of the congruent triangle.

Complete step-by-step answer:
Given: There is a circle provided. Tangent segments have been drawn to it, we need to prove that they are congruent.
As per the given information, we proceed by drawing the figure first.

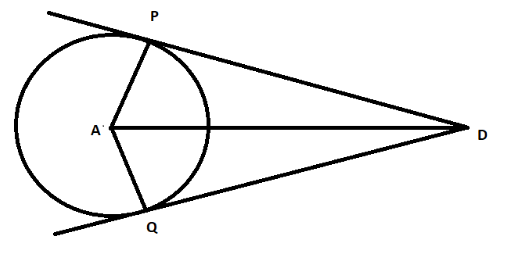
Here, the circle is centered at A. The tangent segments have been drawn to the circle from the external point D. AP and AQ are the straight lines connecting the point of contact P and Q to the centre A. It is thus obvious that the angles APD and AQD are right angles, since as per tangent theorem, we know that they are right angles.
Here, in triangles APD and AQD, line segments PA and QA are congruent, since they are the radii of the same circle.
Again, Segment AD is the common side.
Lastly, the angles APD and AQD are right angles.
Thus, the angles\[\angle APD = \angle AQD = {90^ \circ }\].
So, by the Side Angle Side law of congruency, we can say that the triangles APD and AQD are congruent.
Therefore, \[\angle APD \cong \angle AQD\].
Since two congruent triangles have equal sides, so PD=QD.
Thus it is proved that the tangent segments drawn from an external point to a circle are congruent.

Note: In problems like these, it is to be always remembered that all the information given can be translated into geometrical figures and apply accordingly the properties that can be analysed to find the result.
Also, follow the different conditions of the congruence of the triangles to prove these types of solutions such as –
SSS criteria (Side - Side - Side)
SAS criteria (Side – Angle - Side)
ASA criteria (Angle – Side – Angle)
AAS criteria (Angle – Angle – Side)
RHS criteria (Right angle – Hypotenuse – Side