Question

Prove that: In a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Answer 1

Hint: Consider a right angled triangle ABC, right angled at B and construct a perpendicular to the side AC passing through B. Use the properties related to similarity of triangles to reach a result which might help you to conclude the mentioned statement.

Complete step-by-step answer:
First, we will draw a right angled triangle ABC, right angled at B and construct a perpendicular to the side AC passing through B.

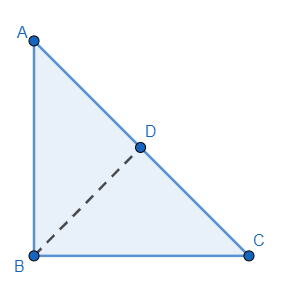
Now in triangle ADB and triangle ABC , we have
Angle A is common between the two triangles, according to our construction $\angle ADB=\angle ABC=90{}^\circ $ . So, by AA similarity criteria, we can say that $\Delta ADB\sim \Delta ABC$ .
Now we know that the ratio of corresponding sides of two similar triangles is constant.
$\therefore \dfrac{AB}{AD}=\dfrac{AC}{AB}$
$\Rightarrow {{\left( AB \right)}^{2}}=AC\times AD..........(i)$
Now in triangle BDC and triangle ABC , we have
Angle B is common between the two triangles, according to our construction $\angle BDC=\angle ABC=90{}^\circ $ . So, by AA similarity criteria, we can say that $\Delta BDC\sim \Delta ABC$ .
Now we know that the ratio of corresponding sides of two similar triangles is constant.
$\therefore \dfrac{DC}{BC}=\dfrac{BC}{AC}$
$\Rightarrow {{\left( BC \right)}^{2}}=AC\times DC..........(ii)$
Now, if we add equation (i) and (ii), we get
${{\left( BC \right)}^{2}}+{{\left( AB \right)}^{2}}=AC\times DC+AC\times AD$
${{\left( BC \right)}^{2}}+{{\left( AB \right)}^{2}}=AC\left( DC+AD \right)$
Now from the figure, we can see that $DC+AD=AC$ . So, our equation becomes:
${{\left( BC \right)}^{2}}+{{\left( AB \right)}^{2}}=AC\times AC$
$\Rightarrow {{\left( BC \right)}^{2}}+{{\left( AB \right)}^{2}}={{\left( AC \right)}^{2}}$
So, we have proved that, in a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Note: The main part in the above solution is the construction of the line BD. Also, it might be difficult to see the similar triangles in case of the above question. However, it is very important that you remember the Pythagoras theorem, as it is used in almost every question related to right angled triangles.