Question

Prove that if two lines intersecting each other, then the vertically opposite angles are equal.

Answer 1

Hint: We start solving the problem by drawing the two lines which were intersecting each other at a fixed point. We then use the fact that the sum of the angles lying on a straight line is equal to ${{180}^{\circ }}$ (which is also known as linear pair axiom) for the angles present on the both lines. We then make the necessary calculations using the relations obtained between the angles present on the two lines to complete the required proof.

Complete step-by-step answer:
According to the problem, we need to prove that if two lines intersect each other, then the vertically opposite angles are equal.
Let us draw the two lines AB and CD intersecting at point O.

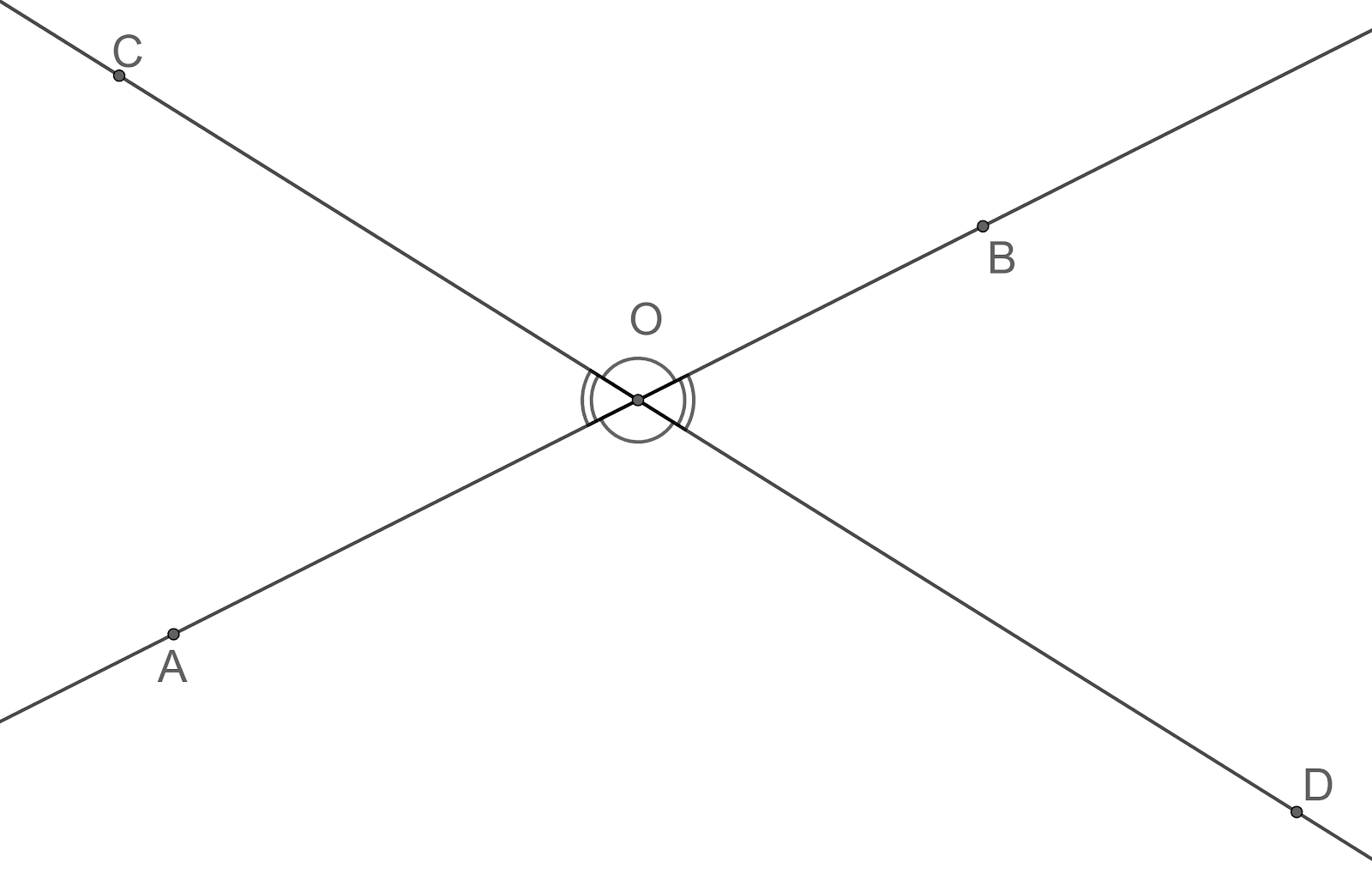
We know that the sum of angles lying on a straight line is ${{180}^{\circ }}$.
Let us consider the angles on the line CD. So, we get $\angle COB+\angle BOD={{180}^{\circ }}$.
$\Rightarrow \angle COB={{180}^{\circ }}-\angle BOD$ ---(1).
Now, let us consider the angles on the line AB. So, we get $\angle COB+\angle AOC={{180}^{\circ }}$ ---(2).
Let us substitute equation (2) in equation (1).
So, we get ${{180}^{\circ }}-\angle BOD+\angle AOC={{180}^{\circ }}$.
$\Rightarrow \angle AOC={{180}^{\circ }}-{{180}^{\circ }}+\angle BOD$.
$\Rightarrow \angle AOC=\angle BOD$.
From the figure, we can see that the angles $\angle AOC$ and $\angle BOD$ are vertically opposite angles.
So, we have proved that if two lines intersect each other, then the vertically opposite angles are equal.

Note: We can also prove that the other pair of vertically opposite angles $\angle COB$ and $\angle DOA$ equal in the similar way as shown below:
Let us consider the angles on the line CD. So, we get $\angle COB+\angle BOD={{180}^{\circ }}$.
$\Rightarrow \angle BOD={{180}^{\circ }}-\angle COB$ ---(3).
Now, let us consider the angles on the line AB. So, we get $\angle BOD+\angle DOA={{180}^{\circ }}$ ---(4).
Let us substitute equation (3) in equation (4).
So, we get ${{180}^{\circ }}-\angle COB+\angle DOA={{180}^{\circ }}$.
$\Rightarrow \angle DOA={{180}^{\circ }}-{{180}^{\circ }}+\angle COB$.
$\Rightarrow \angle DOA=\angle COB$.
We use this result to get the required answers.