Question

Prove that if in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion) then the two triangles are similar.

Answer 1

Hint: We will first draw two random triangles with equal corresponding angles and then draw a line in between the larger one with some condition such that the two new triangles are congruent. We will use the theorem: If a line is drawn parallel to one side of a triangle cutting the other two sides at distinct points, then the sides are divided into equal ratios and then use the componendo method to prove the result.

Complete step-by-step answer:
Let us first draw two triangles to get the proper reference. As per the given condition, we have equal corresponding angles that means $\angle A = \angle D,\angle B = \angle E$ …….(1) and $\angle C = \angle F$ …….(2). Now, draw points P and Q in the bigger triangle such that AB = DP and AC = PQ and join P and Q to form the line PQ as shown below in the figure:-

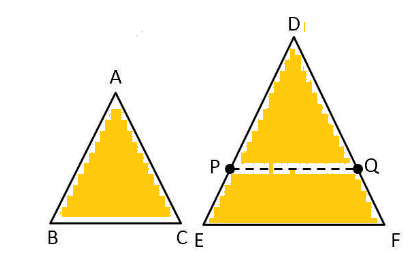
Now, consider the triangle ABC and DPQ:
$\angle A = \angle D$ (given in question)
AB = DP (As per our construction)
AC = DQ (As per our construction)
Therefore, $\vartriangle ABC \cong \vartriangle DPQ$ (By SAS property)
SAS property states that two triangles are congruent if they have two equal corresponding sides and one equal corresponding angle.
So, $\angle B = \angle P$ and $\angle C = \angle Q$ (By CPCT) …………(3)
CPCT stands for Corresponding parts of Congruent triangles. CPCT theorem states that if two or more triangles which are congruent to each other are taken then the corresponding angles and the sides of the triangles are also congruent to each other.
Now, using (1), (2) and (3), we will get:-
$\angle E = \angle P$ and $\angle Q = \angle F$.
For lines PQ and EF with transversal PE, $\angle E$ and $\angle P$ are corresponding angles.
Hence, $PQ||EF$.
Now we will use the theorem: If a line is drawn parallel to one side of a triangle cutting the other two sides at distinct points, then the sides are divided into equal ratios.
Therefore, by applying this theorem in $\vartriangle DEF$, we have:-
$\dfrac{{DP}}{{PE}} = \dfrac{{DQ}}{{QF}}$
Taking reciprocal of the equation, we have:-
$\dfrac{{PE}}{{DP}} = \dfrac{{QF}}{{DQ}}$
Now, adding 1 on both the sides, we will get:-
$\dfrac{{PE}}{{DP}} + 1 = \dfrac{{QF}}{{DQ}} + 1$
Taking LCM to simplify, we have:-
$\dfrac{{PE + DP}}{{DP}} = \dfrac{{QF + DQ}}{{DQ}}$ …….(4)
We can clearly observe from the figure that $PE + DP = DE$ and $QF + DQ = DF$.
Hence, (4) becomes:- $\dfrac{{DE}}{{DP}} = \dfrac{{DF}}{{DQ}}$
Now taking reciprocal again:
$\dfrac{{DP}}{{DE}} = \dfrac{{DQ}}{{DF}}$
As per our construction condition, we can rewrite it as:
$\dfrac{{AB}}{{DE}} = \dfrac{{AC}}{{DF}}$.
Going in the similar way with all the sides, we can get:-
$\dfrac{{AB}}{{DE}} = \dfrac{{AC}}{{DF}} = \dfrac{{BC}}{{EF}}$.
Hence, proved.

Note: The students must note that the statement we just proved is a theorem which is known as AAA criteria for similarity of triangles. If you need to use this result in any other question, you may use it by just mentioning its statement and name.
$AAA- Angle, angle, angle$; $SAS- Side, angle, side$; $SSS- Side, side, side$; $ASA- Angle, side, angle$