Question

Prove that equilateral triangle is equiangular.

Answer 1

Hint: We will use the concept that angles opposite to equal sides of a triangle are equal and we know that all the sides of an equilateral triangle are equal. We will also use the property that the sum of all the three angles of a triangle is equal to 180˚.

Complete step by step solution:
It is given in the question that we have to prove that equilateral triangle is equiangular. Here, equiangular means all the three angles of the equilateral triangle have the same measure.
Now, let us assume an equilateral triangle ABC. We know that all the sides of an equilateral triangle are equal, it means that in triangle ABC, we have AB = BC = AC.

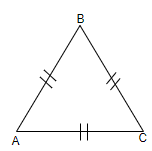
We know that the angles opposite to the equal sides of a triangle are equal. So, here we have the side AB equal to the side AC, it means that $\angle B=\angle C.........\left( i \right)$.
Similarly, we have the side AB equal to the side BC, it means that $\angle C=\angle A.........\left( ii \right)$.
So, from equations (i) and (ii), we get,
$\angle A=\angle B=\angle C$
This means that all the angles of an equilateral triangle are equal.
Now, we know that the sum of all angles of a triangle is equal to 180˚. As all the angles are equal, we can write the equation as,
$\begin{align}
  & \angle A+\angle A+\angle A={{180}^{\circ }} \\
 & 3\angle A={{180}^{\circ }} \\
 & \angle A=\dfrac{{{180}^{\circ }}}{3}={{60}^{\circ }} \\
\end{align}$
As all the angles are equal it means that $\angle A=\angle B=\angle C={{60}^{\circ }}$
Thus, it is proved that the equilateral triangle is equiangular.

Note: Most of the students make mistakes while taking angles while applying the concept that angles opposite to the equal sides of a triangle are equal. For example, we have the sides AB and BC equal, so according to the concept, we will get $\angle A=\angle C$, but some students may write it as $\angle A=\angle B$ which is wrong.