Question

Properties And Uses Of Different Radiations Of Electromagnetic Spectrum

Answer 1

Hint: Electric dipole is a setup of two charges in which two charges of equal magnitude are placed at a very small distance from each other. One must know the true meaning of ‘pole’. Monopole means a system of single charge. Hence the monopole of a system is the net value of charge contained within a region. When considered the system of two charges separated by some distance, it’s called electric dipole.

Formula used:
$\vec p = q(L)\hat L$,$R = \sqrt{A^2+B^2+2ABcos\theta}$and $\alpha =tan^{-1}{ \dfrac{\vec B sin \theta}{\vec B cos \theta + A}}$.

Complete answer:
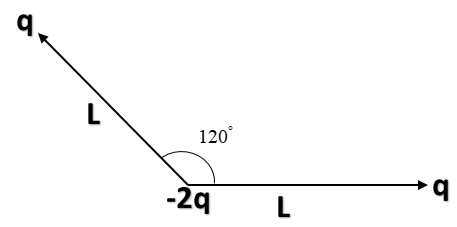
Dipole moment of the system of two charges is denoted by ‘p’ where $\vec p = q(L)\hat L$, and in this formula, we take charge of any one and distance between them. Dipole moment is defined for charges of the same magnitude. It is a vector quantity with direction from +q to –q, which is the meaning of$\hat L$. Now, in the diagram, as the two systems of charges are inclined at some angle, hence we have to perform vector addition to find their resultant.
Now, both the systems of charges have the same dipole moment ‘qL’.
Hence adding them using vector addition.

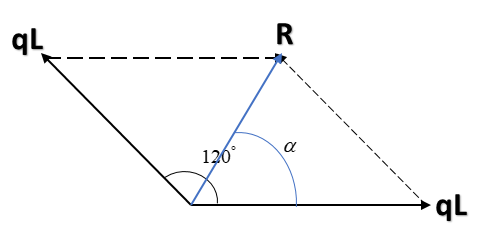
Thus using,$R = \sqrt{A^2+B^2+2ABcos\theta}$, we get;
$R = \sqrt{(qL)^2+(qL)^2+2(qL)(qL)cos120^{\circ}}$
$R = \sqrt{2(qL)^2+2(qL)(qL)\dfrac{-1}{2} }$
$R = \sqrt{2(qL)^2 - (qL)^2} = qL$
Hence the resultant dipole moment of the system is ‘qL’.
Now, using;
$\alpha =tan^{-1}{ \dfrac{\vec B sin \theta}{\vec B cos \theta + A}}$
$\alpha =tan^{-1}{ \dfrac{qL sin 120^{\circ}}{qL cos 120^{\circ} + qL}}$
$\alpha =tan^{-1}{ \dfrac{qL \dfrac{\sqrt 3}{2}}{qL \dfrac{-1}{2}+ qL}} = tan^{-1}\sqrt 3$
Hence, $\alpha = 60^{\circ}$.
Hence, the dipole moment of the system is ‘qL’ acting at an angle $\alpha = 60^{\circ}$ from the x-axis.

Note:
Whenever representing a vector quantity, it’s always mandatory to mention both magnitude and direction of the vector otherwise it will be like a car without wheels. Students are always advised to represent the complete vector while practicing the subject so that it could become a habit. Also, the direction of dipole moment is along the length and directed from negative charge to the positive.