Question

PQ is a tangent drawn from a point P to a circle with center O and QOR is a diameter of the circle such that \[\angle POR = {120^ \circ }\], then find \[\angle OPQ\]
A) \[{60^ \circ }\]
B) \[{45^ \circ }\]
C) \[{30^ \circ }\]
D) \[{90^ \circ }\]

Answer 1

Hint: Here we will use the concept of linear pair which states that the sum of two adjacent angles formed by two intersecting lines is \[{180^ \circ }\].
Also, we will use the concept of angle sum property of triangles which states that the sum of all angles of a triangle is \[{180^ \circ }\]

Complete step-by-step solution:

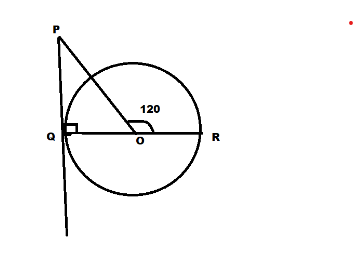
It is given that:-
PQ is a tangent,
QOR is a diameter of the circle and \[\angle POR = {120^ \circ }\]
We know that according to the linear pair property the sum of two adjacent angles formed by two intersecting lines is \[{180^ \circ }\].
Hence,
$\Rightarrow$\[\angle POR + \angle POQ = {180^ \circ }\]
Putting in the given values we get:-
$\Rightarrow$\[{120^ \circ } + \angle POQ = {180^ \circ }\]
Solving for \[\angle POQ\] we get:-
$\Rightarrow$\[\angle POQ = {180^ \circ } - {120^ \circ }\]
Solving it further we get:-
$\Rightarrow$\[\angle POQ = {60^ \circ }\]
Now we know that radius through the point of contact of a tangent to a circle is perpendicular to the tangent.
Therefore, \[\angle PQO = {90^ \circ }\]
Now we know that, angle sum property of triangles which states that the sum of all angles of a triangle is \[{180^ \circ }\]
Applying this property in triangle \[POQ\] we get:-
$\Rightarrow$\[\angle POQ + \angle PQO + \angle OPQ = {180^ \circ }\]
Putting in the respective values we get:-
$\Rightarrow$\[{60^ \circ } + {90^ \circ } + \angle OPQ = {180^ \circ }\]
Simplifying it we get:-
$\Rightarrow$\[{150^ \circ } + \angle OPQ = {180^ \circ }\]
Solving for \[\angle OPQ\] we get:-
$\Rightarrow$\[\angle OPQ = {180^ \circ } - {150^ \circ }\]
$\Rightarrow$\[\angle OPQ = {30^ \circ }\]

Hence the value of required angle is \[{30^ \circ }\]

Note: Students should remember the following property to solve the given question which is the important trick of this question:-
The radius through the point of contact of a tangent to a circle is perpendicular to the tangent.
Also, students can draw the tangent at any point on the circle and then proceed with the problem but note that tangent is the line which touches the circle at only one point.