Question

What is the potential energy of this configuration of three charges?

Answer 1

Hint: In order to solve this question, we are going to firstly analyze the configuration of the three charges and we will find the potential energy of the charges taking two at a time, one by one, then, the total potential energy of the configuration is found by adding the three potential energies as calculated.

Formula used: The potential energy of the two charges is given as:
\[{U_3} = - \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q_1}{q_2}}}{r}\]
Where, \[r\]is the distance between the two charges \[{q_1}\]and\[{q_2}\].


Complete step-by-step solution:
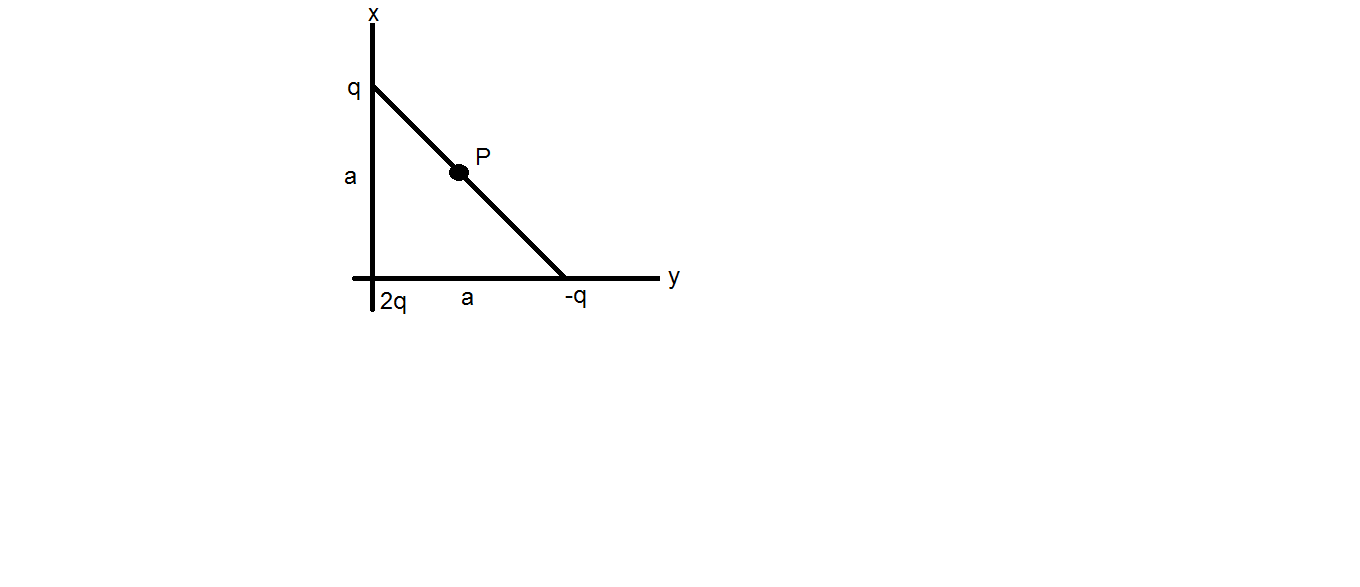
It is given that the three charges are given in the configuration as above, if we find the potential energy taking two charges at a same time then, adding them can give the total potential energy of the configuration.
Let us first take the two charges, \[q\]and\[2q\], which are at a distance of \[a\]
Then, the potential energy is equal to:
\[{U_1} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{2{q^2}}}{a}\]
Now, taking the two charges \[2q\]and\[ - q\], which are at a distance of\[a\]
Then, the potential energy is equal to:
\[{U_2} = - \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{2{q^2}}}{a}\]
Taking the other two charges, \[q\]and\[ - q\], the distance between them is found by Pythagoras theorem,
\[s = \sqrt {{a^2} + {a^2}} = \sqrt 2 a\]
Thus, potential energy is given by
\[{U_3} = - \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{{q^2}}}{a}\]
Therefore, the total potential energy is equal to the sum of the three as given by:
\[U = {U_1} + {U_2} + {U_3} = \dfrac{1}{{4\pi {\varepsilon _0}}}\left( {\dfrac{{2{q^2}}}{a} - \dfrac{{2{q^2}}}{a} - \dfrac{{{q^2}}}{{\sqrt 2 a}}} \right)\]
Solving this equation, we get,
\[U = \dfrac{{ - {q^2}}}{{4\sqrt 2 \pi {\varepsilon _0}a}}\]

Note:It is important to note that the potential energy is the energy held by an object because of its position relative to other objects, stresses within itself, its electric charge, or other factors. It is taken for two charges at a time when more than the two charges are given, then the potential energies are found taking two charges each one by one.