Question

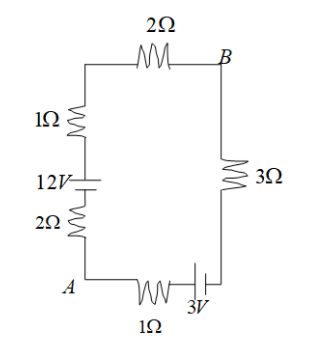
Potential difference ${V_B} - {V_A}$ in the network shown is ?

Answer 1

Hint: From the given circuit the equivalent resistance has to be calculated by noticing the connections of the resistors. The potential difference between the two given points is required. So, the equivalent emf of the circuit is required. To find this, the formula of equivalent emf is to be concluded in which the given values of battery and calculated equivalent resistance are used.

Formula used:
The equivalent resistance for two series resistors ${R_1}$ and ${R_{2,}}
$\[R = {R_1} + {R_2}\]
And, The equivalent resistance for two parallel resistors ${R_1}$ and ${R_{2,}}
$\[\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}\]
The formula of equivalent emf:
$\dfrac{{{E_{eq}}}}{{{R_{eq}}}} = \dfrac{{{E_1}}}{{{R_1}}} + \dfrac{{{E_2}}}{{{R_2}}}$

Complete step by step answer:
Let, \[{R_1} = 2\Omega \], \[{R_2} = 1\Omega \], \[{R_3} = 2\Omega \], \[{R_4} = 3\Omega \] and \[{R_5} = 1\Omega \]. From the circuit, it is seen that ${R_1},{R_2}$ and ${R_3}$ are connected in series.So, the equivalent resistance for these series resistors is,
$R' = {R_1} + {R_2} + {R_3} = 2 + 1 + 2 = 5\Omega $
And, ${R_4}$ and ${R_5}$ are connected in series.
So, the equivalent resistance for these series resistors is,
$R'' = {R_4} + {R_5} = 3+1 = 4\Omega$

Now, the $R'$ and $R''$ are connected in parallel.
So, $\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{R'}} + \dfrac{1}{{R''}}$
$ \Rightarrow {R_{eq}} = \dfrac{{R' \times R''}}{{R' + R''}} = \dfrac{{20}}{9}$
The formula of equivalent emf:
$\dfrac{{{E_{eq}}}}{{{R_{eq}}}} = \dfrac{{{E_1}}}{{R'}} + \dfrac{{{E_2}}}{{R''}}$ given that, ${E_1} = 12V$ and ${E_2} = 3V$
$ \Rightarrow \dfrac{{{E_{eq}}}}{{\dfrac{{20}}{9}}} = \dfrac{{12}}{5} + \dfrac{3}{4}$
$ \Rightarrow {E_{eq}} = \dfrac{{63}}{{20}} \times \dfrac{{20}}{9}$
$ \therefore {E_{eq}} = 7{\text{ volt}}$

Hence, the potential difference between point A and B, ${V_B} - {V_A} = 7{\text{ volt}}$.

Note: Kirchhoff's law for any closed system states that the total voltage drop between two points is equal to the addition of all the potential drops individually between the same two points. The unit of potential drop that occurs between two points is Volt and is defined as being the potential difference dropped across a certain resistance of one ohm with a current of one ampere passing through it. The electric potential difference is also called voltage. It is the work that is applied externally needed to bring a charge from one place to another place in an electric field. Electric potential difference is the change of potential energy of a unit positive charge.