Question

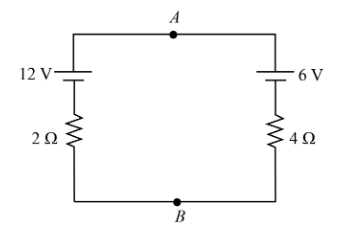
Potential difference across AB, i.e.,${V_A} - {V_B}$ is

(1). $10\;{\rm{V}}$
(2). $8\;{\rm{V}}$
(3). $6\;{\rm{V}}$
(4). zero

Answer 1

Hint: In the solution we will use the Kirchhoff’s second law in both the loops. Also Ohm’s law is employed to find the current passing through the circuit. When a circuit is considered we have to include all the parameters that are included in the circuit.

Complete step by step answer:
Given is the circuit with two cells each of $12\;{\rm{V}}$ and $6\;{\rm{V}}$ with corresponding resistances $2\;\Omega $ and $4\;\Omega $ respectively.
Let us suppose that the current passing through the circuit is $i$.
From Ohm's law, we know, $V = iR$, where $V$ is the voltage, $i$ is the current and $R$ is the resistance. Therefore applying this, to the two resistances, we have,
The voltage across the resistance $2\;\Omega $ is $V = 2i$ and the voltage across the resistance $4\;\Omega $ is $V = 4i$
As we know that, according to Kirchhoff’s second law, in any closed loop network, the total voltage around the loop is equal to the sum of all the voltage drops within the same loop. This means that the total voltage within the loop is equal to zero. Starting at any point in the loop continues in the same direction noting the direction of all the voltage drops, either positive or negative, and returning back to the same starting point. It is important to maintain the same direction either clockwise or anti-clockwise or the final voltage sum will not be equal to zero. We can use Kirchhoff’s voltage law when analysing series circuits.
Hence from the given loop we have,
$
\Rightarrow 12\;{\rm{V}} - 6\;{\rm{V}} - 4i - 2i = 0\\
\Rightarrow 6\;{\rm{V}} = 6i\\
\Rightarrow i = 1\;{\rm{A}}
$
Thus the voltage across the resistance $4\;\Omega $ is $V = 4\;\Omega \times 1\;{\rm{A}} = 4\;{\rm{V}}$.
Now applying the Kirchhoff’s law to the right side of the loop starting from A to B through $4\;\Omega $, we have,
$
{V_A} - 6\;{\rm{V}} - 4\;{\rm{V}} - {V_B} = 0\\
\therefore{V_A} - {V_B} = 10\;{\rm{V}}
$
Therefore the Potential difference across AB, i.e.,${V_A} - {V_B}$ is $10\;{\rm{V}}$.
Hence,option (1) is the correct answer.

Note: Make sure to calculate the voltage through the resistance. All the voltages in the loops are to be considered while applying Kirchhoff's law. When a loop is considering, make sure that the loop is counted in the same way, either clockwise or anticlockwise in all the cases.