Question

When the polynomial $\left( 6{{x}^{4}}+8{{x}^{3}}+17{{x}^{2}}+21x+7 \right)$ is divided by $\left( 3{{x}^{2}}+4x+1 \right)$ the remainder is $\left( ax-b \right)$. Therefore,
\[\begin{align}
  & A.a=1,b=2 \\
 & B.a=1,b=-2 \\
 & C.a=2,b=1 \\
 & D.a=-1,b=-2 \\
\end{align}\]

Answer 1

Hint: In this question, we are given two polynomials and we need to divide them to find the remainder. For this, we will use the long division method. We will first learn all the steps involved and then solve our sum.

Complete step by step answer:
We are given the polynomial as $\left( 6{{x}^{4}}+8{{x}^{3}}+17{{x}^{2}}+21x+7 \right)$ and $\left( 3{{x}^{2}}+4x+1 \right)$. For dividing them, let us use the following steps.
Step 1: Let us make sure that, polynomial is written in descending order. Now let us divide the term with highest power inside the division symbol by the term with the highest power outside the division symbol.
Step 2: Let us multiply the answer obtained in the previous step by the polynomial in front of the division symbol.
Step 3: Let us subtract and bring down the next term.
Step 4: Repeating steps 1, 2, 3 until there are no terms to bring down, we get

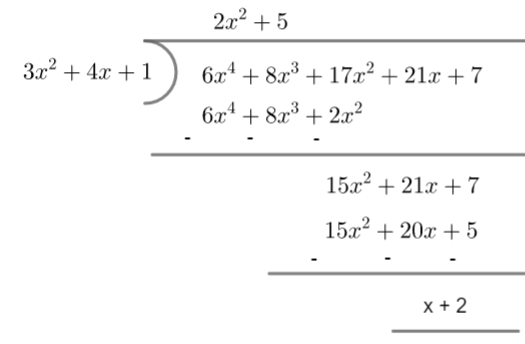
As we can see from the long division method that, the remainder is x+2. Comparing it with ax+b we can see that a = 1 and b = 2. So required values of a and b are 1 and 2 respectively.

So, the correct answer is “Option A”.

Note: Students can make mistakes of signs in these sums. They can get confused between quotient and remainder. Remember that, division is in the form of $Di\overset{Q}{\overline{\left){\begin{align}
  & D \\
 & \overline{R} \\
\end{align}}\right.}}$ where Di is divisor, D is dividend, Q is quotient and R is remainder. Before starting the division make sure that dividend is in descending order. Put the 0 for missing power of x to evaluate easily. Make sure that the degree of remainder is less than the degree of the divisor otherwise we need to proceed further.