Question

Points I, II and III in the following plot respective correspond to: (\[{V_{mp}}\]: most probable velocity).

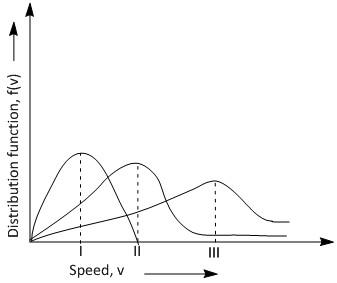
A. \[{V_{mp}}\] of \[{N_2}\] (\[300K\]); \[{V_{mp}}\] of \[{H_2}\] (\[300K\]); \[{V_{mp}}\] of \[{O_2}\] (\[400K\])
B. \[{V_{mp}}\] of \[{H_2}\] (\[300K\]); \[{V_{mp}}\] of \[{N_2}\] (\[300K\]); \[{V_{mp}}\] of \[{O_2}\] (\[400K\])
C. \[{V_{mp}}\] of \[{O_2}\] (\[300K\]); \[{V_{mp}}\] of \[{N_2}\] (\[300K\]); \[{V_{mp}}\] of \[{H_2}\] (\[400K\])
D. \[{V_{mp}}\] of \[{N_2}\] (\[300K\]); \[{V_{mp}}\] of \[{O_2}\] (\[300K\]); \[{V_{mp}}\] of \[{H_2}\] (\[400K\])

Answer 1

Hint: The most probable velocity of a gas is defined as the velocity that is possessed by the maximum fraction of gas molecules which are at the same temperature.

Complete step by step answer:
The most probable velocity was described by the Maxwell-Boltzmann distribution. The speed of gas molecules which corresponds to the maximum number of molecules is known as most probable velocity. For this a graph was given by Maxwell known as a distribution graph which demonstrates the velocity of gas molecules at their maximum.
The given figure indicates the Maxwell-Boltzmann distribution of velocities for different gases at a various temperatures, such as hydrogen at \[300K\] and \[400K\], nitrogen at \[300K\] and oxygen at \[300K\] and\[400K\] . The velocity at the top of the curve mentioned by the positions I, II, and III is called the most probable velocities of the respective gases as the maximum numbers of molecules have that speed.
The most probable velocity is mathematically expressed using the formula:
\[{V_{mp}} = \sqrt {\dfrac{{2RT}}{M}} \] , where \[{V_{mp}}\] is most probable velocity for the molecule with molar mass \[M\] , \[R\] is the gas constant , \[T\] is the temperature, \[M\] is the molecular weight of the gas.
From the above relation, it is clear that the most probable velocity is directly proportional to the temperature and inversely proportional to the molar mass of gas molecules.
The molar mass of the given gases varies in the order:
\[{M_{{H_2}}} = 2 < {M_{{N_2}}} = 28 < {M_{{O_2}}} = 32\]
Thus \[{V_{mp}}\] of \[{H_2}\] at \[300K\] and \[400K\] are , $Vmp = \sqrt {\dfrac{{2R \times 400}}{2}} = 20\sqrt R $ and $Vmp = \sqrt {\dfrac{{2R \times 300}}{2}} = 17.32\sqrt R $
\[{V_{mp}}\] of \[{N_2}\] at \[300K\], $Vmp = \sqrt {\dfrac{{2R \times 300}}{{28}}} = 4.63\sqrt R $
\[{V_{mp}}\] of \[{O_2}\] at \[300K\] and \[400K\] are, $Vmp = \sqrt {\dfrac{{2R \times 400}}{{32}}} = 5\sqrt R $ and $Vmp = \sqrt {\dfrac{{2R \times 300}}{{32}}} = 4.33\sqrt R $

Hence the order of the most probable velocity is in the order, \[{V_{mp}}\] of \[{O_2}\] (\[300K\]); \[{V_{mp}}\] of \[{N_2}\] (\[300K\]); \[{V_{mp}}\] of \[{H_2}\] (\[400K\]) , i.e. option C is the correct answer.

Note: According to the Maxwell-Boltzmann distribution function the molecules are considered in random motion. The molecules move in different directions with constant velocities. The collisions of a molecule with other gas molecules and with the walls of the container results in chaotic motion and there is no change of the energies after collision.