
Point charges +4q, -q, +4q are kept on the x-axis at points x=0, x=a , x=2a respectively .then ,
A. Only q is in stable equilibrium
B. None of the charges are in equilibrium
C. All the charges are in unstable equilibrium
D. All the charges are in stable equilibrium
Answer
566.1k+ views
Hint: Just like we used newton’s inverse square law to find out the gravitational force of interaction between the two masses, we have coulomb’s law to find out the electrostatic force of interaction between the two charges. When forces are balanced we call that charge is in equilibrium.
Formula used:
$F = \dfrac{{k{q_1}{q_2}}}{{{r^2}}}$
Complete step by step answer:
Three charges are kept at various positions on the x axis. The distance between any two charges is the same. 4q is kept at origin and -q is kept at a distance on x axis and another 4q is kept at 2a distance on the x axis. The given situation is illustrated in the below diagram
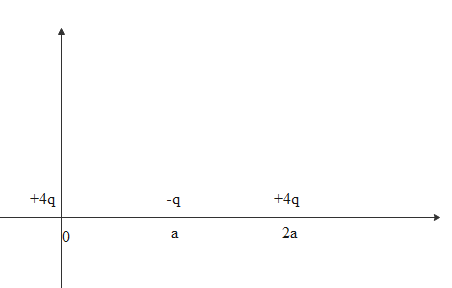
Between any two charges there will be force. It is given by the coulomb’s law
$F = \dfrac{{k{q_1}{q_2}}}{{{r^2}}}$
Where k is the coulomb constant and ${q_1},{q_2}$ are charges and ‘r’ is the distance between them
Force on the charge -q will be due to the other two charges 4q and 4q
$F = \dfrac{{k{q_1}{q_2}}}{{{r^2}}}$
$\eqalign{
& \Rightarrow F = \dfrac{{k4q( - q)}}{{{a^2}}} - \left( {\dfrac{{k4q( - q)}}{{{a^2}}}} \right) \cr
& \therefore F = 0 \cr} $
The reason why we negative sign i.e subtract one force from the other is because both are acting in the opposite directions on -q charge.
Force on the charge 4q at x=0 will be due to the other two charges -q and 4q
$F = \dfrac{{k{q_1}{q_2}}}{{{r^2}}}$
$\eqalign{
& \Rightarrow F = \left| {\dfrac{{k4q( - q)}}{{{a^2}}}} \right| - \left| {\left( {\dfrac{{k4q(4q)}}{{{{(2a)}^2}}}} \right)} \right| \cr
& \Rightarrow F = \dfrac{{k4q(q)}}{{{a^2}}} - \dfrac{{k4q( q)}}{{{a^2}}} \cr
& \therefore F = 0 \cr} $
Force on the charge 4q at x=2a will be due to the other two charges -q and 4q
$F = \dfrac{{k{q_1}{q_2}}}{{{r^2}}}$
$\eqalign{
& \Rightarrow F = \left| {\dfrac{{k4q( - q)}}{{{a^2}}}} \right| - \left| {\left( {\dfrac{{k4q(4q)}}{{{{(2a)}^2}}}} \right)} \right| \cr
& \Rightarrow F = \dfrac{{k4q(q)}}{{{a^2}}} -\dfrac{{k4q( q)}}{{{a^2}}} \cr
& \therefore F = 0 \cr} $
Hence force on all charges is zero. Hence all charges are in equilibrium. If we move charge -q in any direction then force in that direction becomes dominant and it continues to move in the same direction. Same happens with the remaining charges too.
If displacement and restoring force are in opposite directions to each other then that is stable equilibrium. But here they are in the same direction. So all charges are in unstable equilibrium.
Hence option C is the correct answer.
Note:
Stable and unstable equilibrium can be clearly understood with our daily day examples too. If we put a ball in the bowl then it is in stable equilibrium as its potential energy is least. If we put the ball on the bowl then it is in unstable equilibrium as its potential energy will be very high. Everything tries to attain the least energy state.
Formula used:
$F = \dfrac{{k{q_1}{q_2}}}{{{r^2}}}$
Complete step by step answer:
Three charges are kept at various positions on the x axis. The distance between any two charges is the same. 4q is kept at origin and -q is kept at a distance on x axis and another 4q is kept at 2a distance on the x axis. The given situation is illustrated in the below diagram
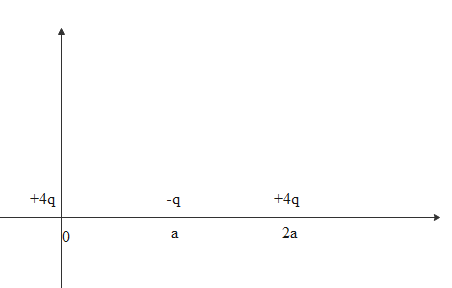
Between any two charges there will be force. It is given by the coulomb’s law
$F = \dfrac{{k{q_1}{q_2}}}{{{r^2}}}$
Where k is the coulomb constant and ${q_1},{q_2}$ are charges and ‘r’ is the distance between them
Force on the charge -q will be due to the other two charges 4q and 4q
$F = \dfrac{{k{q_1}{q_2}}}{{{r^2}}}$
$\eqalign{
& \Rightarrow F = \dfrac{{k4q( - q)}}{{{a^2}}} - \left( {\dfrac{{k4q( - q)}}{{{a^2}}}} \right) \cr
& \therefore F = 0 \cr} $
The reason why we negative sign i.e subtract one force from the other is because both are acting in the opposite directions on -q charge.
Force on the charge 4q at x=0 will be due to the other two charges -q and 4q
$F = \dfrac{{k{q_1}{q_2}}}{{{r^2}}}$
$\eqalign{
& \Rightarrow F = \left| {\dfrac{{k4q( - q)}}{{{a^2}}}} \right| - \left| {\left( {\dfrac{{k4q(4q)}}{{{{(2a)}^2}}}} \right)} \right| \cr
& \Rightarrow F = \dfrac{{k4q(q)}}{{{a^2}}} - \dfrac{{k4q( q)}}{{{a^2}}} \cr
& \therefore F = 0 \cr} $
Force on the charge 4q at x=2a will be due to the other two charges -q and 4q
$F = \dfrac{{k{q_1}{q_2}}}{{{r^2}}}$
$\eqalign{
& \Rightarrow F = \left| {\dfrac{{k4q( - q)}}{{{a^2}}}} \right| - \left| {\left( {\dfrac{{k4q(4q)}}{{{{(2a)}^2}}}} \right)} \right| \cr
& \Rightarrow F = \dfrac{{k4q(q)}}{{{a^2}}} -\dfrac{{k4q( q)}}{{{a^2}}} \cr
& \therefore F = 0 \cr} $
Hence force on all charges is zero. Hence all charges are in equilibrium. If we move charge -q in any direction then force in that direction becomes dominant and it continues to move in the same direction. Same happens with the remaining charges too.
If displacement and restoring force are in opposite directions to each other then that is stable equilibrium. But here they are in the same direction. So all charges are in unstable equilibrium.
Hence option C is the correct answer.
Note:
Stable and unstable equilibrium can be clearly understood with our daily day examples too. If we put a ball in the bowl then it is in stable equilibrium as its potential energy is least. If we put the ball on the bowl then it is in unstable equilibrium as its potential energy will be very high. Everything tries to attain the least energy state.
Recently Updated Pages
In the figure AB BC CD DE EF FG GA then angle DAE is class 12 maths CBSE

How will you bring about the following conversations class 12 chemistry CBSE

DNA replication is A Continuous and conservative B class 12 biology CBSE

The binding energy of nucleus is given by Eb Delta class 12 physics CBSE

In an astronomical telescope of normal adjustment a class 12 physics CBSE

The relation between algae and fungi in a lichen is class 12 biology CBSE

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

The pH of the pancreatic juice is A 64 B 86 C 120 D class 12 biology CBSE

Give 10 examples of unisexual and bisexual flowers




