Question

Plot the points \[(3,5)\] and \[(-1,3)\] , and verify from the graph that the straight line joining these points passes through\[(1,4)\].

Answer 1

Hint: The \[x\] coordinate of a point determines its distance from the \[y\] axis and the \[y\] coordinate of the point determines its distance from the \[x\] axis , use this knowledge to mark the respective points on the graph .

Complete step-by-step answer:

Before plotting the points , we must know about the coordinate system.
The cartesian coordinate system is a system of identifying the location of a point with respect to two perpendicular lines , known as coordinate axes. The vertical axis is called the \[y\] axis and the horizontal axis is called the \[x\] axis. The point of intersection of these axes is called the origin and it is represented by the ordered pair \[(0,0)\]. The distance of a point from the \[y\] axis is called the \[x\]coordinate and the distance of the point from \[x\] axis is called the \[y\] coordinate of the point.
Now , coming to the question , the point \[(3,5)\]represents a point which is at the distance of \[3\]units from the \[y\] axis in the positive \[x\] direction and \[5\]units from the \[x\] axis in the positive \[y\] direction.
Similarly , the point \[(-1,3)\] represents a point which is at the distance of \[1\] units from the \[y\] axis in the negative \[x\] direction and \[3\] units from the \[x\] axis in the positive \[y\] direction.
So , the points can be plotted on the graph as:

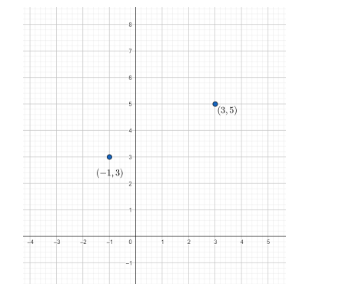
Now , we will join the points \[(3,5)\] and \[(-1,3)\] with a line.

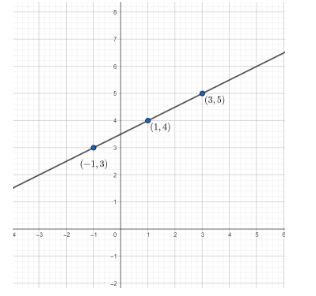
We can clearly see that the point \[(1,4)\] lies on the line joining the points \[(3,5)\] and \[(-1,3)\] .
So , we can say that the line joining the points \[(3,5)\] and \[(-1,3)\] passes through the point \[(1,4)\] .

Note: The \[x\] coordinate of a point is also known as “abscissa” and the \[y\] coordinate of a point is also known as “ordinate”.