Question

Plot a graph showing the variation of Coulomb force (F) versus \[\dfrac{1}{{{r}^{2}}}\], where r is the distance between the two charges of each pair of charge (\[1\mu C,2\mu C\]) and (\[1\mu C,-3\mu C\]). Interpret the graphs thus obtained.

Answer 1

Hint: We need to find the Coulomb’s force acting on the pair of charges using the given information. Using this, we can plot the graphs for each case and understand the differences and similarities between the charge pairs and forces acting on them.

Complete answer:
We know that Coulomb's law relates the charges and the distance between them to find the force between them. It states that the force is proportional to the product of the charges and inversely proportional to the square of the distance between them as –
\[F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{1}}{{q}_{2}}}{{{r}^{2}}}\]
Now, let us consider the given pairs one-by-one –
1.The charges of \[(1\mu C,2\mu C)\] at a distance ‘r’: The force acting between them is given by –
\[\begin{align}
  & F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{2\times {{10}^{-12}}}{{{r}^{2}}} \\
 & \Rightarrow F\propto \dfrac{18\times {{10}^{-3}}}{{{r}^{2}}}N \\
\end{align}\]
The graph can be given as –
         

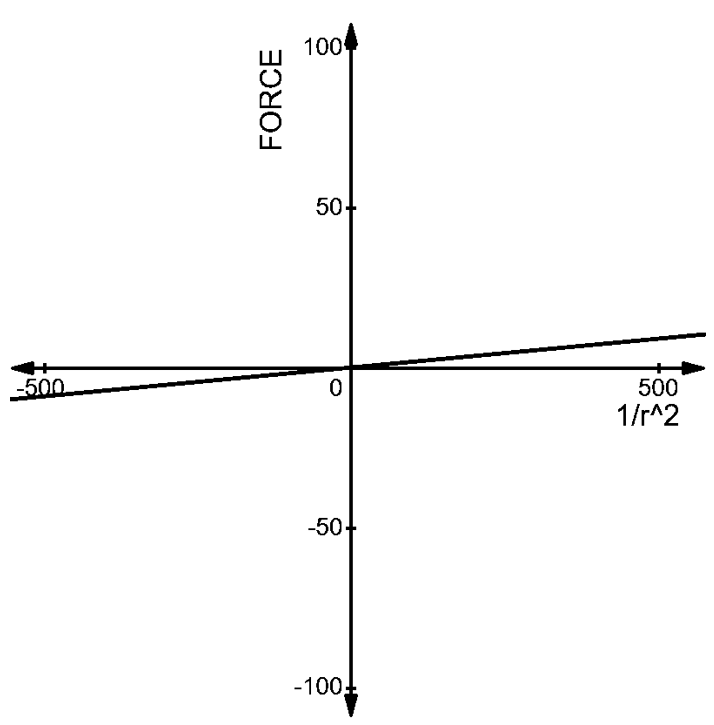
2. The charges of \[(1\mu C,-3\mu C)\]at a distance of ’r’ from each other has a force acting on each other given by –
\[\begin{align}
  & F=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{-3\times {{10}^{-12}}}{{{r}^{2}}} \\
 & \Rightarrow F\propto \dfrac{-27\times {{10}^{-12}}}{{{r}^{2}}} \\
\end{align}\]
The graph of this pair is given by –
   

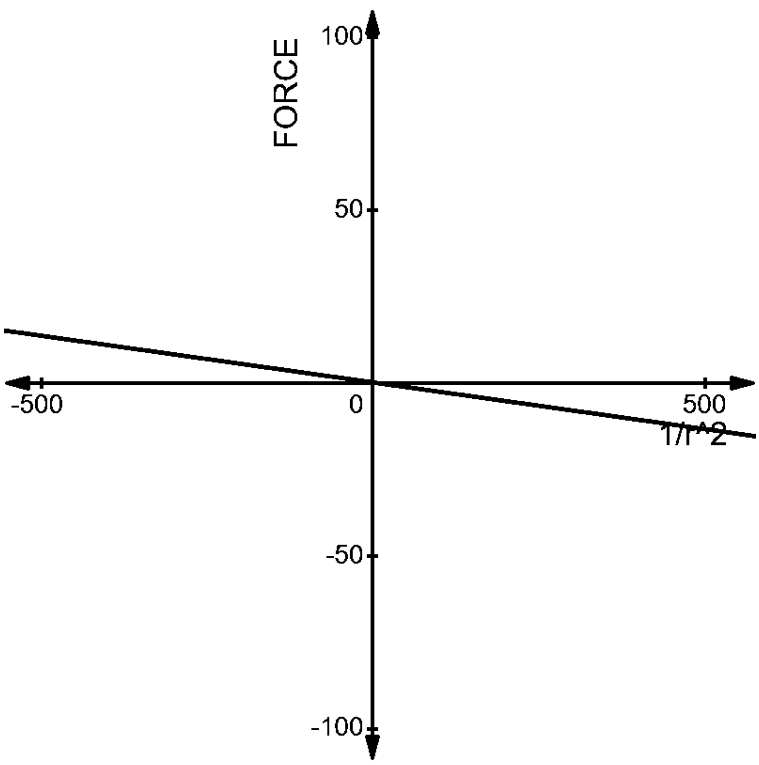
Now, let us compare the two graphs. We can understand very easily, that the force acting on both the pairs are opposite to each other.
The net force in case 1 is positive, whereas the net force in the case 2 is negative as shown below -
 

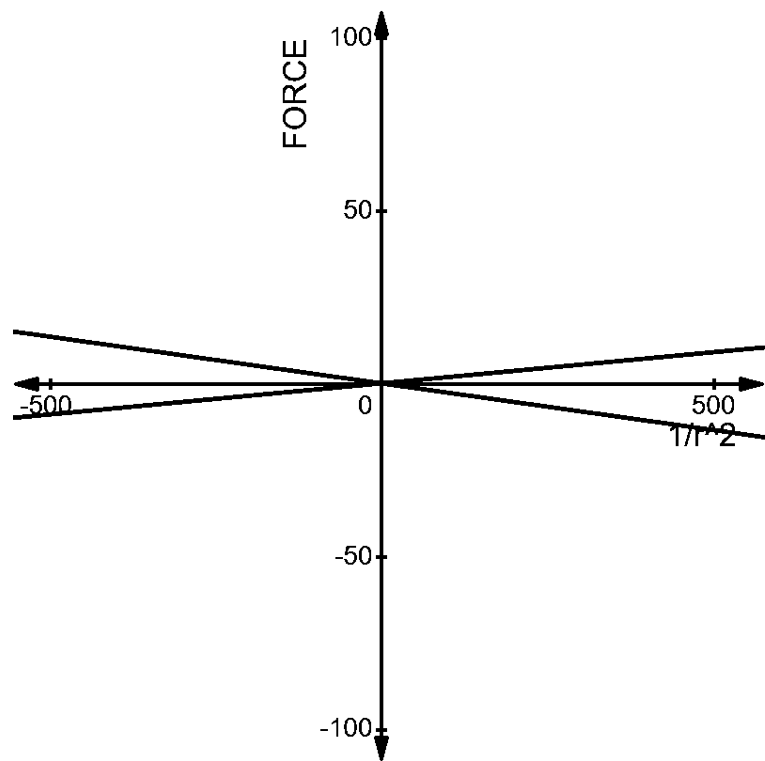
The change in the direction of the force in the two situations are due to the signs of the charge present in the two pairs. The first pair has a net positive charge, which results in repulsion between the charges.
The second pair has a net negative force between them, which results in the attraction of two charges. These two inferences are as we expected, i.e., the like charges repel and the unlike charges attract.
We can infer these from the two graphs.

Note:
The inverse proportionality of the distance and the force between the charge is highly visible from the graph. The Coulomb’s force acting on the pair of charge is therefore, directly proportional to the factor \[\dfrac{1}{{{r}^{2}}}\] and the graph is a straight line with a constant slope.