Question

How can I physically generate a square with two $\text{4x4}$ squares, three $\text{3x3}$ squares, four $\text{2x2}$ squares and $4$ $\text{1x1}$ squares?

Answer 1

Hint: In this question we will first write the total area we have by using the area of the square formula which is $a={{s}^{2}}$ where $a$ is the area of the square and $s$ is the length of the side of the square. We will then find the total area which we have from all the given squares and then try to fit a square which can have all or some squares in it.

Complete step by step solution:
We have the squares given as two $\text{4x4}$ squares, three $\text{3x3}$ squares, four $\text{2x2}$ squares and four $\text{1x1}$ squares?
Now on using the formula of the area of a square and then multiplying it with the number of squares present, we will get the total area.
Therefore, the area is:
$\Rightarrow 2\times \left( 4\times 4 \right)=32$ units
$\Rightarrow 3\times \left( 3\times 3 \right)=27$ units
$\Rightarrow 4\times \left( 2\times 2 \right)=16$ units
$\Rightarrow 4\times \left( 1\times 1 \right)=4$ units
Now the total area is:
$\Rightarrow 32+27+16+4=79$ units.
Now we know that a square with the area of $79$ units cannot be made using the provided set of squares.
The greatest possible number which has an integer square root which is lesser than $79$ is a square with $64$ square units. Now a square of $64$ units has a length of $8$ units.
Now even though it is a perfect square, there exists no possible combination of squares such that they create another greater square.
The only square that can be created from the given sets of squares is a square of $49$ units which has a side of $7$ units. The square can be made up as:

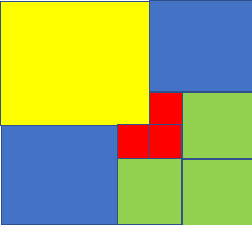
Where the yellow square represents the $\text{4x4}$ square, blue squares represent $\text{3x3}$ squares, green squares represent $\text{2x2}$ squares and red squares represent $\text{1x1}$ squares.

Note: It is to be remembered that we have not used some of the squares provided to us because upon inserting them, we would have not got a perfect square. It is to be noted that the area of the square is $49$ units therefore the area unused is $79-49=30$ units.