Question

Periodic time of a satellite revolving above Earth’s surface at a height equal to R (radius of earth) is (g is the acceleration due to gravity at Earth’s surface) –
\[\begin{align}
  & \text{A) 2}\pi \sqrt{\dfrac{2R}{g}} \\
 & \text{B) 4}\sqrt{2}\pi \sqrt{\dfrac{R}{g}} \\
 & \text{C) 2}\pi \sqrt{\dfrac{R}{g}} \\
 & \text{D) 8}\pi \sqrt{\dfrac{R}{g}} \\
\end{align}\]

Answer 1

Hint: We need to understand the relation between the orbital radius of the satellite, the earth’s radius, and the acceleration due to gravity at different heights to solve the periodic time taken for revolution by the satellite that is required in this problem.

Complete step-by-step solution
Satellites revolve around the Earth in fixed orbits with a fixed time period. The force acting on the satellite due to the gravitational force of the earth is balanced by the centripetal force by maintaining a fixed velocity which is given as –
\[\begin{align}
  & {{F}_{C}}={{F}_{g}} \\
 & \Rightarrow \dfrac{m{{v}^{2}}}{r}=\dfrac{GMm}{{{r}^{2}}} \\
 & \therefore v=\sqrt{\dfrac{GM}{r}} \\
\end{align}\]

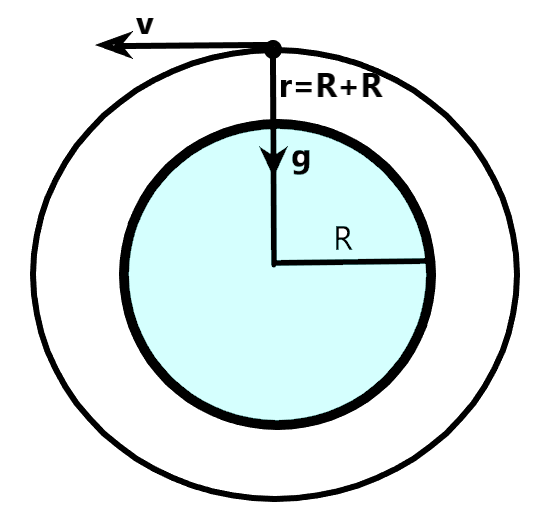
We also know that the acceleration due to gravity acting on a body on the surface of the earth can be solved by equating the force due to mass of the object and the gravitational force as –
\[\begin{align}
  & {{F}_{g}}={{F}_{m}} \\
 & \Rightarrow \dfrac{GMm}{{{R}^{2}}}=mg \\
 & \therefore g=\dfrac{GM}{{{R}^{2}}} \\
\end{align}\]
Now, we know that the time taken for the satellite to complete one complete revolution around the earth can be determined by dividing the length of the journey in revolution by the velocity of the satellite in the orbit, which we have found earlier. We can find the time period of revolution from this relation as –
\[\begin{align}
  & T=\dfrac{l}{v} \\
 & \text{but,} \\
 & l=2\pi r \\
 & \Rightarrow T=\dfrac{2\pi r}{v} \\
 & \Rightarrow T=\dfrac{2\pi r}{\sqrt{\dfrac{GM}{r}}} \\
 & \therefore T=2\pi \sqrt{\dfrac{{{r}^{3}}}{GM}} \\
\end{align}\]
Now, we need to substitute the value of the product of the gravitational constant ‘G’ and the mass of earth ‘M’ with the acceleration due to gravity as –
\[\begin{align}
  & T=2\pi \sqrt{\dfrac{{{r}^{3}}}{GM}} \\
 & \text{but,} \\
 & g{{R}^{2}}=GM \\
 & \Rightarrow T=2\pi \sqrt{\dfrac{{{r}^{3}}}{g{{R}^{2}}}} \\
 & \text{Also,} \\
 & r=R+R \\
 & \Rightarrow T=2\pi \sqrt{\dfrac{{{(2R)}^{3}}}{g{{R}^{2}}}} \\
 & \therefore T=4\sqrt{2}\pi \sqrt{\dfrac{R}{g}} \\
\end{align}\]
This is the required time period of revolution of the satellite.
The correct answer is option B.

Note: The satellites are kept in an orbit by maintaining a discrete velocity in such a way that the satellite will not possess too much energy to escape from the Earth’s field or too low that it falls down to the planet. In fact, an orbit is defined as an energy level in space.