Question

Period of \[\cos x\cos ({60^ \circ } - x)\cos ({60^ \circ } + x)\] is
\[A.)\] \[\dfrac{\pi }{2}\]
\[B.)\] \[\dfrac{\pi }{3}\]
\[C.)\] \[\dfrac{{2\pi }}{3}\]
\[D.)\] \[\pi \]

Answer 1

Hint: Here we have to find out the period of the given equation. Also, we use the trigonometric formulas for finding this. On doing some simplification we get the required answer.

Formula used: Following formulas are applicable in the question:
\[2\cos A\cos B = \cos (A + B) + \cos (A - B)\].
We will use the following trigonometric formulas:
\[4{\cos ^3}(x) - 3\cos (x) = \cos (3x)\] .
\[\cos (2x) = 2{\cos ^2}x - 1\] .
Also, the period of a function, \[f(x) = \cos (kx)\] is \[\dfrac{{2\pi }}{{\left| k \right|}}\].

Complete step-by-step solution:
Let us consider, \[f(x) = \cos x\cos ({60^ \circ } - x)\cos ({60^ \circ } + x)\]
Now, we will try to simplify the given equation to apply the formula:
\[ \Rightarrow f(x) = \cos x\dfrac{1}{2}(2\cos ({60^ \circ } - x)\cos ({60^ \circ } + x))\]
Again we use the formula, we can split it up into following form:
\[ \Rightarrow f(x) = \cos x\left( {\dfrac{{\cos ({{60}^ \circ } + x + {{60}^ \circ } - x) + \cos ({{60}^ \circ } + x - {{60}^ \circ } - x)}}{2}} \right)\] .
Now, cancel the opposite sign, we get:
\[ \Rightarrow f(x) = \cos x\left( {\dfrac{{\cos ({{120}^ \circ }) + \cos (2x)}}{2}} \right).....\left( 1 \right)\] .
Now, we have to find the value and we get,

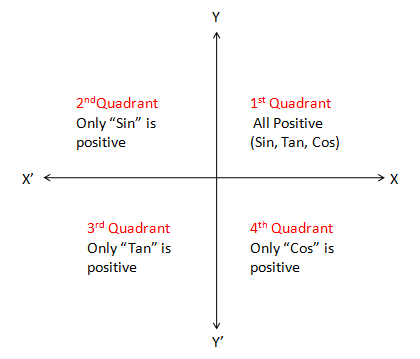
We can interpret \[\cos ({120^ \circ }) = \cos ({90^ \circ } + {30^ \circ })\].
So, \[\cos ({120^ \circ })\] comes in \[{2^{nd}}\] quadrant.
So, in the \[{2^{nd}}\] quadrant \[\cos \] will change in \[\sin \], but it will have negative signs before it.
So, \[\cos ({120^ \circ }) = \cos ({90^ \circ } + {30^ \circ }) = - \sin ({30^ \circ }) = - \dfrac{1}{2}\].
So, the value of \[\cos ({120^ \circ })\] is\[\left( { - \dfrac{1}{2}} \right)\].
Put this value in the \[\left( 1 \right)\] equation, we get:
\[ \Rightarrow f(x) = \cos x\left( {\dfrac{{\left( { - \dfrac{1}{2}} \right) + \cos (2x)}}{2}} \right)\] .
Taking LCM on the numerator term and we get,
\[ \Rightarrow f(x) = \cos x\left( {\dfrac{{\dfrac{{ - 1 + 2\cos (2x)}}{2}}}{2}} \right)\]
Taking reciprocal we get,
\[ \Rightarrow f(x) = \cos x\left( {\dfrac{{2\cos (2x) - 1}}{4}} \right)\] .
Putting the trigonometric formula of \[\cos (2x) = 2{\cos ^2}x - 1\]in the above equation, we get:
\[ \Rightarrow f(x) = \cos x\left( {\dfrac{{2\left( {2{{\cos }^2}x - 1} \right) - 1}}{4}} \right)\]
On multiply the bracket term and we get
\[ \Rightarrow f(x) = \cos x\left( {\dfrac{{\left( {2(2{{\cos }^2}(x)) - (2 \times 1} \right) - 1}}{4}} \right)\] .
Multiplying the constant terms and subtracting them, we get the following equation:
\[ \Rightarrow f(x) = \cos x\left( {\dfrac{{4{{\cos }^2}(x) - 3}}{4}} \right)\] .
By doing multiplication to the rest of the terms, we get the following equation:
\[ \Rightarrow f(x) = \left( {\dfrac{{4{{\cos }^3}(x) - 3\cos (x)}}{4}} \right)\] .
Putting the trigonometric formula of \[4{\cos ^3}(x) - 3\cos (x) = \cos (3x)\] in the above equation, we get:
\[ \Rightarrow f(x) = \left( {\dfrac{{\cos (3x)}}{4}} \right)\] .
By comparing \[\cos (kx)\] and \[f(x) = \left( {\dfrac{{\cos (3x)}}{4}} \right)\], we can say that \[k\] has a value of \[3\].
So, the period of the given function is, \[f(x) = \dfrac{{2\pi }}{{\left| k \right|}} = \dfrac{{2\pi }}{3}\]

\[\therefore \] Option C is the correct option.

Note: Domain of a cosine function are all in real numbers and where the numbers end in graphs to make a cycle is called the cosine period of the function.
We always need to remember that we have to take the mod of \[k\] in period as the numbers in the graph we can move to the positive side as well as to the negative side.