Question

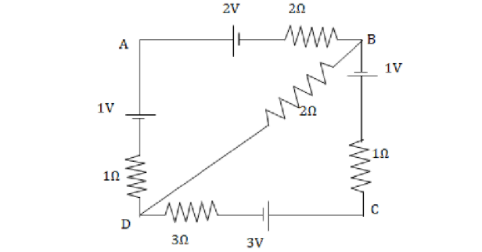
What is the P.D between B and D?

A. \[\dfrac{1}{{13}}\,{\text{V}}\]
B. \[\dfrac{2}{{13}}\,{\text{V}}\]
C. \[\dfrac{7}{{13}}\,{\text{V}}\]
D. \[\dfrac{6}{{13}}\,{\text{V}}\]

Answer 1

Hint:At first simply the circuit by assigning current to the branches. Recall Kirchhoff’s first law and Kirchhoff’s second law. Use this law to find current through the branches and then use the value of current to find the potential difference of the given branch.

Complete step by step solution:
We are asked to find the voltage or potential difference between point B and D.
Let us \[i\] be flowing in the branch DC and the same current will flow through branch BC.
Now, at point B we apply Kirchhoff’s first law or junction law according to which current leaving a junction is equal to current entering a junction.
Let \[{i_1}\] be the current flowing through branch BD then according to Kirchhoff’s first law \[\left(
{i - {i_1}} \right)\] current will flow through branch AB.

Now, we apply Kirchhoff’s voltage rule according to which the sum of voltages of a closed loop is equal to zero.

Applying Kirchhoff’s voltage rule to loop ABDA we have,
\[ - 1 - 1\left( {i - {i_1}} \right) + 2{i_1} - 2\left( {i - {i_1}} \right) + 2 = 0\]
\[ \Rightarrow 3i - 5{i_1} = 1\] (i)
Applying Kirchhoff’s voltage rule to loop DCBA, we have
\[ - 3i + 3 - 1 - 1i - 2{i_1} = 0\]
\[ \Rightarrow 4i + 2{i_1} = 2\]
\[ \Rightarrow 2i + {i_1} = 1\] (ii)
Multiplying equation (i) with \[2\], we get
\[6i - 10{i_1} = 2\] (iii)
Multiplying equation (ii) with \[3\], we get
\[6i + 3{i_1} = 3\] (iv)
Now, subtracting equation (iii) from (iv), we get
\[13{i_1} = 1 \\
\Rightarrow {i_1} = \dfrac{1}{{13}} \]
Resistance on branch BD is \[2\Omega \] and current is \[\dfrac{1}{{13}}\,{\text{A}}\], so potential difference between B and D will be
\[V = {\text{(Resistance)(current)}} \\
\Rightarrow V = 2 \times \dfrac{1}{{13}} = \dfrac{2}{{13}}\,{\text{V}} \]

Hence, the correct answer is option (B) \[\dfrac{2}{{13}}\,{\text{V}}\].

Note: There are two Kirchhoff’s laws which are used to find the value of current and voltage of circuits. The first law is Kirchhoff’s current law or junction law which states that the sum current entering and leaving a junction of an electrical circuit is always zero. The second law or also known as voltage law states that the sum of the voltage drops around any closed circuit is always zero.