Question

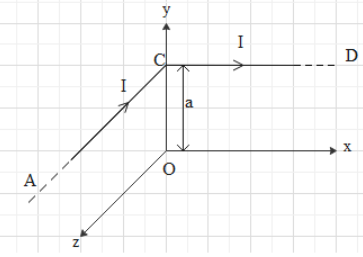
Part AC and DC of a conductor are parallel to z-axis and x-axis respectively as shown in figure. The magnitude of magnetic field at point O has magnitude
               

\[\begin{align}
  & \text{A) }\dfrac{{{\mu }_{0}}I}{2\pi a} \\
 & \text{B) }\dfrac{{{\mu }_{0}}I}{2\sqrt{2}\pi a} \\
 & \text{C) }\dfrac{2\sqrt{2}{{\mu }_{0}}I}{\pi a} \\
 & \text{D) }\dfrac{{{\mu }_{0}}I}{4\sqrt{2}\pi a} \\
\end{align}\]

Answer 1

Hint: We have to find the magnitude of the magnetic field at point O for the given diagram. Now there are two conductors in which one is parallel to the z-axis whereas the other is parallel to x-axis. So we can find the magnetic field at O along the z-axis and x-axis with the help of Ampere’s law.
Formula used:
\[B=\dfrac{{{\mu }_{0}}I}{4\pi r}\]

Complete answer:
From the given diagram we can see that there is a common point at C which is distanced ‘a’ from the point O and lying on the y-axis. Also the part AC and CD are perpendicular to the y-axis as well as AC is also perpendicular to CD.
Now according to Ampere’s law (for magnetic field), magnetic field of the conductor is given by
\[B=\dfrac{{{\mu }_{0}}I}{4\pi r}\]
Where I is the current flowing through the conductor, r is the radius of the conductor and \[{{\mu }_{0}}\]is the permeability of the conductor.
If we consider the part AC which is lying parallel to z-axis and distance of it from Point O is a then the magnetic field at point O along the z-axis will be given as
\[{{B}_{z}}=\dfrac{{{\mu }_{0}}I}{4\pi a}\overset{\wedge }{\mathop{k}}\,\]
Similarly for the part of conductor CD parallel to x-axis, the magnetic field at point O due to it, will be
\[{{B}_{x}}=\dfrac{{{\mu }_{0}}I}{4\pi a}\overset{\wedge }{\mathop{i}}\,\]
Now we have asked the magnetic of the magnetic field at point O, which will be given as
\[\begin{align}
  & B=\sqrt{B_{x}^{2}+B_{z}^{2}} \\
 & B=\sqrt{{{\left( \dfrac{{{\mu }_{0}}I}{4\pi a} \right)}^{2}}+{{\left( \dfrac{{{\mu }_{0}}I}{4\pi a} \right)}^{2}}} \\
 & B=\sqrt{{{\left( \dfrac{{{\mu }_{0}}I}{4\pi a} \right)}^{2}}(1+1)} \\
 & B=\dfrac{{{\mu }_{0}}I}{4\pi a}\sqrt{2} \\
 & B=\dfrac{{{\mu }_{0}}I}{2\sqrt{2}\pi a} \\
\end{align}\]

Hence option B is the correct option.

Note:
As there is no plane or conductor parallel to the y-axis, so there is no need to add the y component of the magnetic field. Also while calculating magnitude the vector components are not taken. The Ampere law used here is for the magnetic field inside the conductor as given data is for part of the conductor.