Question

Out of $ 40 $ students, $ 14 $ are taking mathematics and $ 29 $ are taking physics. How many students are in either class if $ 5 $ students are in both classes?
A. $ 2 $
B. $ 4 $
C. $ 6 $
D. $ 8 $

Answer 1

Hint: We have to solve the question the given question is the part of set theory, the given question will be solved with the help of the venn diagrams, the venn diagrams for the given situation will be drawn and then we will find the conclusion of our question, which is to find the number of students not present in none of the classes mathematics or physics.

Complete step-by-step answer:
The situation is given as,
Total students are $ 40 $ ,
the students of mathematics are $ 14 $
the students of physics are $ 29 $ ,
 $ 5 $ students are present in both classes,
The venn diagram will be shown by the diagram given below,

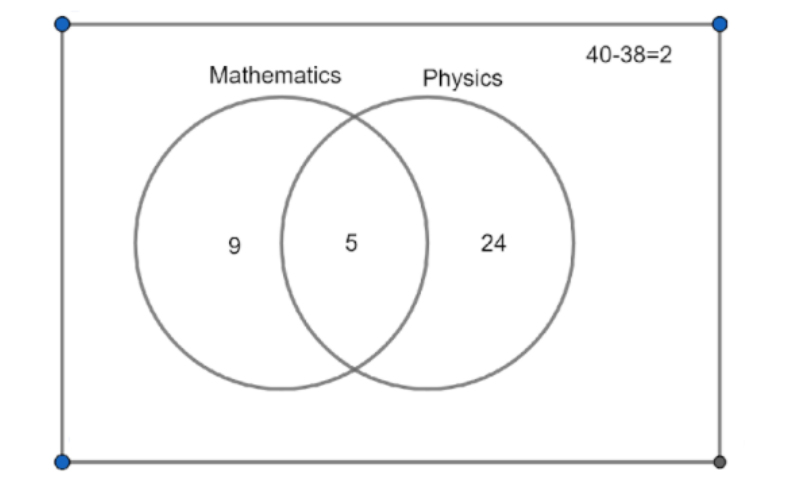
The diagram given above tells that out of total $ 14 $ students in mathematics, there were $ 5 $ common students, the same is the case with the mathematics out of $ 29 $ students $ 5 $ were common and thus the total number of students having at least one class are,
 $ \Rightarrow 14 + 9 + 24 $
 $ \Rightarrow 38 $
Since the total no. of people were $ 40 $
The remaining students $ 2 $ are not in any class be it physics or mathematics. This is mentioned in the diagram given above.

Note: The given question could have also been solved by the formula,
 $ n(A \cup B) = n(A) + n(B) - n(A \cap C) $
Here $ n(A) = 14 $ and $ n(B) = 29 $ and $ n(A \cap B) = 5 $
When we get the value of $ n(A \cup B) $ as $ 38 $ , we will get the value of $ n'(A \cup B) $ as $ 2 $ to get the final value of the students which are not present in either class be it physics or mathematics class.